练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．某学校有若干学生社团，其中“文学社”、“围棋社”、“书法社”的人数分别为9、18、27．现采用分层抽样的方法从这三个社团中抽取6人外出参加活动．
    （1）求应从这三个社团中分别抽取的人数；
    （2）将抽取的6人进行编号，编号分别为A1，A2，A3，A4，A5，A6，现从这6人中随机地抽出2人组成活动小组．
    ①用所给编号列出所有可能的结果；
    ②设A为事件“编号为A1和A2的2人中恰有1人被抽到”，求事件A发生的概率．

    分析 （1）由题意可得抽取比例，可得相应的人数；
    （2）列举可得从6名人员中随机抽取2名的所有结果共15种；事件A包含上述8个，由概率公式可得．

    解答 解：（1）应从“文学社”、“围棋社”、“书法社”中抽取的人数分别是：1，2，3，
    （2）①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为：
    （A1，A2），（A1，A3），（A1，A4），（A1，A5），（A1，A6），
    （A2，A3），（A2，A4），（A2，A5），（A2，A6），（A3，A4），
    （A3，A5），（A3，A6），（A4，A5），（A4，A6）），（A5，A6），共15种．
    ②事件A包含：（A1，A3），（A1，A4），（A1，A5），（A1，A6），
    （A2，A3），（A2，A4），（A2，A5），（A2，A6）），共8个基本事件．
    因此，事件A发生的概率P（A）=$\frac{8}{15}$．

    点评 本题考查古典概型及其概率公式，涉及分层抽样，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．已知正项数列{an}的首项a1=1，且（n+1）a${\;}_{n+1}^{2}$+anan+1-na${\;}_{n}^{2}$=0对?n∈N*都成立．
    （1）求{an}的通项公式；
    （2）记bn=a2n-1a2n+1，数列{bn}的前n项和为Tn，证明：Tn＜$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若直线ax+y-2=0与圆心为C的圆（x-1）2+（y-a）2=16相交于A，B两点，且$\overrightarrow{CA}•\overrightarrow{CB}=0$，则实数a的值是-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．某公司有A、B、C、D、E五辆汽车，其中A、B两辆汽车的车牌尾号均为1，C、D两辆汽车的车牌尾号均为2，E车的车牌尾号为6．已知在非限行日，每辆车可能出车或不出车，A、B、E三辆汽车每天出车的概率均为$\frac{2}{3}$，C、D两辆汽车每天出车的概率均为$\frac{1}{2}$，五辆汽车是否出车相互独立，该公司所在地区汽车限行规定如下：
    工作日星期一星期二星期三星期四星期五
    限行车牌尾号0和51和62和73和84和9
    例如，星期一禁止车牌尾号为0和5的车辆通行．
    （1）求该公司在星期一至少有2辆汽车出车的概率；
    （2）设X表示该公司在星期二和星期三两天出车的车辆数之和，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．某四棱台的三视图如图所示，则该四棱台的体积是（　　）
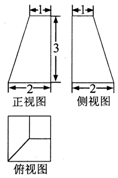
    A．7B．6C．5D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数y=$\frac{3x}{x-1}$的值域为{y|y≠3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在平面直角坐标系式xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1（-c，0）、F2（c，0），已知（1，e）和（e，$\frac{\sqrt{3}}{2}$）都在椭圆上，其中e为椭圆的离心率．
    （1）求椭圆C的方程；
    （2）过点F2的直线l与椭圆C相交于P，Q两点，且$\overrightarrow{P{F}_{2}}$•$\overrightarrow{{F}_{1}Q}$+$\overrightarrow{{F}_{1}{F}_{2}}$•$\overrightarrow{Q{F}_{2}}$=4，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列命题中，正确的是（　　）
    A．若a＞b，c＞d，则ac＞bdB．若ac＞bc，则a＞b
    C．若a＞b，c＞d，则a-c＞b-dD．若$\frac{a}{{c}^{2}}$＜$\frac{b}{{c}^{2}}$，则a＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下面几种推理中是演绎推理的为（　　）
    A．科学家利用鱼的沉浮原理制造潜艇
    B．猜想数列$\frac{1}{1×2}$，$\frac{1}{2×3}$，$\frac{1}{3×4}$，…的通项公式为an=$\frac{1}{n（n+1）}$（n∈N+）
    C．半径为r的圆的面积S=πr2，则单位圆的面积S=π
    D．由平面直角坐标系中圆的方程为（x-a）2+（y-b）2=r2，推测空间直角坐标系中球的方程为（x-a）2+（y-b）2+（z-c）2=r2

    查看答案和解析>>

    同步练习册答案