
| A. | 若a>b,c>d,则ac>bd | B. | 若ac>bc,则a>b | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b |
分析 A,要满足a>b,c>d,才能得到ac>bd;
B,c<0时,由ac>bc,得a>b;
C,若a>b,c>d,则a-c>b-d或a-c<b-d或a-c=b-d;
D,若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则$\frac{1}{{c}^{2}}>0$,则a<b;
解答 解:对于A,要满足a>b,c>d,才能得到ac>bd,故错;
对于B,c<0时,由ac>bc,得a>b,故错;
对于C,若a>b,c>d,则a-c>b-d或a-c<b-d或a-c=b-d,故错;
对于D,若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则$\frac{1}{{c}^{2}}>0$,则a<b,故正确;
故选:D.
点评 本题考查了不等式的性质及其应用,属于基础题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
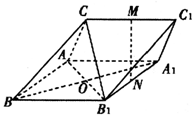 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
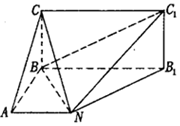 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com