
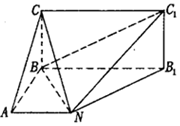
 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.分析 (1)证明BC⊥平面ABB1N,建立空间坐标系,利用向量证明BN⊥NB1,NB⊥B1C1,故而得出结论;
(2)求出两平面的法向量,计算法向量的夹角即可得出二面角的大小.
解答  (1)证明:∵四边形BB1C1C是矩形,∴BC⊥BB1,
(1)证明:∵四边形BB1C1C是矩形,∴BC⊥BB1,
∵平面BB1C1C⊥底面ABB1N,平面BB1C1C∩底面ABB1N=BB1,BC?平面BB1C1C,
∴BC⊥平面ABB1N,
以B为原点,以BA,BB1,BC为坐标轴建立空间直角坐标系B-xyz,
设AB=1,则B(0,0,0),N(1,1,0),B1(0,2,0),C1(0,2,1),C(0,0,1)
∴$\overrightarrow{BN}$=(1,1,0),$\overrightarrow{N{B}_{1}}$=(-1,1,0),$\overrightarrow{{B}_{1}{C}_{1}}$=(0,0,1),
∴$\overrightarrow{BN}•\overrightarrow{N{B}_{1}}$=-1+1=0,$\overrightarrow{BN}•\overrightarrow{{B}_{1}{C}_{1}}$=0,
∴BN⊥NB1,BN⊥B1C1,又NB1∩B1C1=B1,
∴BN⊥平面C1B1N.
(2)解:$\overrightarrow{N{C}_{1}}$=(-1,1,1),$\overrightarrow{NC}$=(-1,-1,1),$\overrightarrow{C{C}_{1}}$=(0,2,0),
设平面BNC1的法向量为$\overrightarrow{m}$=(x,y,z),则$\overrightarrow{m}•\overrightarrow{BN}=0$,$\overrightarrow{m}•\overrightarrow{N{C}_{1}}$=0,
∴$\left\{\begin{array}{l}{x+y=0}\\{-x+y+z=0}\end{array}\right.$,令x=1得$\overrightarrow{m}$=(1,-1,2),
同理可得平面CNC1的法向量为$\overrightarrow{n}$=(1,0,1),
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{2}$.
∴二面角C-C1N-B的大小为30°.
点评 本题考查了线面垂直的判定,空间向量在立体几何中的应用,空间角的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
| 工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则ac>bd | B. | 若ac>bc,则a>b | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 科学家利用鱼的沉浮原理制造潜艇 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$+$\sqrt{3}$ | D. | $\frac{1}{2}$+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com