
分析 (I)由题意,在男生甲被选中的情况下,只需要从其余5人中选出2人,在男生甲被选中的情况下,女生乙也被选中,即从其余4人中选1人即可,即可得出概率.
(II)ξ=0,1,2.利用P(ξ=k)=$\frac{{∁}_{4}^{3-k}{∁}_{2}^{k}}{{∁}_{6}^{3}}$即可得出.
解答 解:(I)由题意,在男生甲被选中的情况下,只需要从其余5人中选出2人,
在男生甲被选中的情况下,女生乙也被选中,即从其余4人中选1人即可,
∴P=$\frac{{∁}_{4}^{1}}{{∁}_{5}^{2}}$=$\frac{2}{5}$.
(II)ξ=0,1,2.P(ξ=k)=$\frac{{∁}_{4}^{3-k}{∁}_{2}^{k}}{{∁}_{6}^{3}}$.
P(ξ=0)=$\frac{1}{5}$,P(ξ=1)=$\frac{3}{5}$,P(ξ=2)=$\frac{1}{5}$.
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了条件概率计算公式、超几何分布列与数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
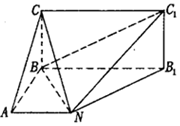 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
| 优秀 | 不优秀 | 合计 | |
| 数学 | |||
| 物理 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com