
【题目】如图,三棱锥![]() 中,
中,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
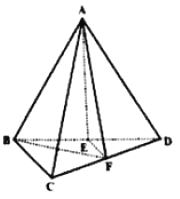
(1)求证:![]() 平面
平面![]() ;
;
(2)已知![]() ,求三棱锥
,求三棱锥![]() 的高.
的高.
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足 ![]() ,(n∈N*),且a1=f(0),则下列结论成立的是( )
,(n∈N*),且a1=f(0),则下列结论成立的是( )
A.f(a2013)>f(a2016)
B.f(a2014)>f(a2015)
C.f(a2016)<f(a2015)
D.f(a2014)<f(a2016)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:
①a:b:c=4:5:6 ②a:b:c=2: ![]() ③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
其中成立的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是一个公差大于0的等差数列,且满足![]() ,a2+a7=16
,a2+a7=16
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式![]() (n∈N*),求数列{bn}的前n项和Sn.
(n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,
,
(1)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程:
的方程:
(2)过定点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,以
两点,以![]() 三点(
三点(![]() 为坐标原点)为顶点作平行四边形
为坐标原点)为顶点作平行四边形![]() ,若点
,若点![]() 刚好在曲线
刚好在曲线![]() 上,求直线
上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
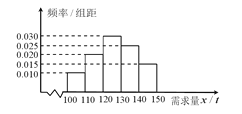
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com