
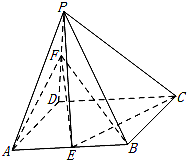
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD的中点.分析 (Ⅰ)作FM∥CD交PC于M,连接ME.证明AF∥EM,然后证明直线AF∥平面PEC.
(Ⅱ)连接ED,证明AB⊥平面PEF.求出三角形PEF的面积,利用VP-BEF=VB-PEF求解即可.
解答 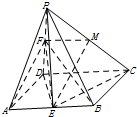 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)证明:作FM∥CD交PC于M,连接ME. …(1分)
∵点F为PD的中点,∴$FM_=^{∥}\frac{1}{2}CD$,
又$AE_=^{∥}\frac{1}{2}CD$,∴$AE_=^{∥}FM$,∴四边形AEMF为平行四边形,∴AF∥EM,…(2分)
∵AF?平面PEC,EM?平面PEC,…(3分)
∴直线AF∥平面PEC. …(4分)
(Ⅱ)连接ED,在△ADE中,AD=1,$AE=\frac{1}{2}$,∠DAE=60°,
∴ED2=AD2+AE2-2AD×AE×cos60°=${1^2}+{({\frac{1}{2}})^2}-2×1×\frac{1}{2}×\frac{1}{2}=\frac{3}{4}$,∴$ED=\frac{{\sqrt{3}}}{2}$,
∴AE2+ED2=AD2,∴ED⊥AB. …(5分)
PD⊥平面ABCD,AB?平面ABCD,∴PD⊥AB,…(6分)
PD∩ED=D,PD?平面PEF,ED?平面PEF,…(7分)
∴AB⊥平面PEF. …(8分)
${S_{△PEF}}=\frac{1}{2}×PF×ED=\frac{1}{2}×\frac{1}{2}×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{8}$,…(9分)
∴三棱锥P-BEF的体积:VP-BEF=VB-PEF …(10分)
=$\frac{1}{3}×{S_{△PEF}}×BE$…(11分)
=$\frac{1}{3}×\frac{{\sqrt{3}}}{8}×\frac{1}{2}$=$\frac{{\sqrt{3}}}{48}$. …(12分)
点评 本题考查空间几何体的体积,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
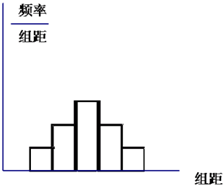 按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.
按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $±\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈[0,$\frac{π}{2}$],sinx0+cosx0≥2 | B. | ?x∈(3,+∞),x2>2x+1 | ||
| C. | ?x0∈R,x02+x0=-1 | D. | ?x∈R,tanx≥sinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com