
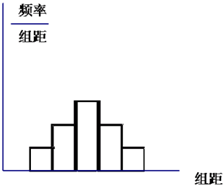
 按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.
按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.分析 (1)根据概率加法公式以及等差数列计算即可;(2)根据概率公式计算即可.
解答 解:(1)这5组的频率从左到右依次记做:a1,a2,a3,a4,a5
由频率的性质的:${a_1}+{a_2}+\frac{1}{2}{a_3}=0.5,{a_1},{a_2},{a_3}成等差数列$,设公差为:d
所以:${a_1}+({a_1}+d)+\frac{1}{2}({{a_1}+2d})=0.5$,∴d=0.2
所以∴a3=a1+2d=0.44
第三组的频数:f3=50×0.44=22
即第三组的人数为:22人
(2)由(1)a2=a4=a1+d=0.24,f4=50×0.24=12
即第四组有12人.
所以,从50人中随机选出两人做代表,这两人分别来自第三组和第四组的概率$P=\frac{22}{50}×\frac{12}{49}=\frac{132}{1025}$.
点评 本题考查了概率、等差数列问题,考查频率分别直方图,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | M一定在直线AC上 | B. | M一定在直线CD上 | ||
| C. | M可能在AC上,也可能在BD上 | D. | M不在AC上,也不在BD上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,E为PD的中点,AB=2,∠ABC=$\frac{π}{3}$.
如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,E为PD的中点,AB=2,∠ABC=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
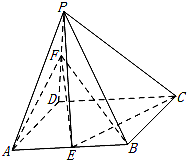 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com