
分析 (1)顺序给定,利用除法进行计算;
(2)每个学校至少一个名额,则分去7个,剩余3个名额分到7所学校的方法种数就是要求的分配方法种数,分类讨论,可得结论.
解答 解:(1)8个人并排站成一排,有${A}_{8}^{8}$种方法,甲乙丙的顺序有${A}_{3}^{3}$种方法,所以甲必须在乙的左边,乙必须在丙的右边,有$\frac{{A}_{8}^{8}}{{A}_{3}^{3}}×2$=13440;
(2)每个学校至少一个名额,则分去7个,剩余3个名额分到7所学校的方法种数就是要求的分配方法种数.
分类:若3个名额分到一所学校有7种方法;
若分配到2所学校有${C}_{7}^{2}$×2=42(种);
若分配到3所学校有${C}_{7}^{3}$=35(种).
∴共有7+42+35=84(种)方法.
点评 本题考查排列组合知识的运用,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-1,3) | C. | (3,1) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
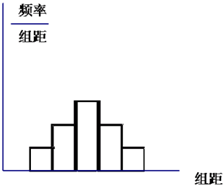 按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.
按某种规定,一个50人的样本频率分布直方图如图.第一组的频率面积为0.04,若前三组的频率与后三组的频率各自构成等差数列,且公差为相反数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
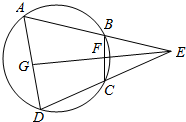 如图,已知四边形ABCD内接于圆,延长AB和DC相交于E,EG平分∠E,且与BC,AD分别相交于F,G.证明:
如图,已知四边形ABCD内接于圆,延长AB和DC相交于E,EG平分∠E,且与BC,AD分别相交于F,G.证明:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com