
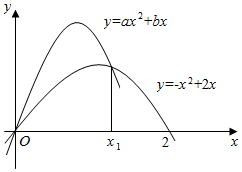 已知y=ax2+bx(a<0)通过点(1,2),且其图象与y=-x2+2x的图象有二个交点(如图所示).
已知y=ax2+bx(a<0)通过点(1,2),且其图象与y=-x2+2x的图象有二个交点(如图所示).分析 (Ⅰ)有已知可得其中一个交点是原点,把另一个交点表示出来,再利用定积分把面积表示处理即可;
(Ⅱ)结合(I)利用导数求解.
解答 解:(Ⅰ)由y=ax2+bx通过点(1,2)可得a+b=2
即b=2-a,由$\left\{\begin{array}{l}y=a{x^2}+bx\\ y=-{x^2}+2x\end{array}\right.$,解得${x_1}=\frac{a}{1+a}$
则y=ax2+bx与y=-x2+2x所围成的面积S与a的函数关系为$S=\int_0^{x_1}{[{(a{x^2}+bx)-(-{x^2}+2x)}]}dx=-\frac{a^3}{{6{{(1+a)}^2}}}$
(Ⅱ)由$S=-\frac{a^3}{{6{{(1+a)}^2}}}$,得$S'=-\frac{1}{6}•\frac{{{a^2}(a+1)(a+3)}}{{{{(1+a)}^4}}}$,
由S'=0得a=-3,a=-1,
当a=-1时,两曲线只有一个交点,不合题意.
当a<-3,S'<0,当a>-3S'>0,
所以当a=-3时,S取得极小值,即最小值,此时b=2-a=5,${S_{min}}=\frac{9}{8}$.
点评 本题主要考查二次函数以及定积分,导数的应用,属于中等题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{e}$) | B. | (0,$\frac{1}{e+1}$] | C. | (0,$\frac{1}{e}$] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∨q”为假 | B. | “p∧q”为真 | C. | p真q假 | D. | p假q真 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com