
| A. | (-1,$\frac{1}{e}$) | B. | (0,$\frac{1}{e+1}$] | C. | (0,$\frac{1}{e}$] | D. | (0,1) |
分析 曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.设P(t,f(t))(t>0),则Q(-t,t3+t2),运用向量垂直的条件:数量积为0,构造函数h(x)=(x+1)lnx(x≥e),运用导数判断单调性,求得最值,即可得到a的范围.
解答 解:假设曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.
不妨设P(t,f(t))(t>0),则Q(-t,t3+t2),∵△POQ是以O为直角顶点的直角三角形,
∴$\overline{OP}$•$\overline{OQ}$=0,即-t2+f(t)(t3+t2)=0 ①.
若方程①有解,存在满足题设要求的两点P、Q;若方程①无解,不存在满足题设要求的两点P、Q.
若0<t<e,则f(t)=-t3+t2代入①式得:-t2+(-t3+t2)(t3+t2)=0,
即t4-t2+1=0,而此方程无解,因此t≥e,此时f(t)=alnt,
代入①式得:-t2+(alnt)(t3+t2)=0,
即$\frac{1}{a}$=(t+1)lnt ②,令h(x)=(x+1)lnx(x≥e),
则h′(x)=lnx+1+$\frac{1}{x}$>0,∴h(x)在[e,+∞)上单调递增,
∵t≥e,∴h(t)≥h(e)=e+1,∴h(t)的取值范围是[e+1,+∞).
∴对于0<a≤$\frac{1}{e+1}$,方程②总有解,即方程①总有解.
故答案为:(0,$\frac{1}{e+1}$].
点评 本题考查分段函数的运用,注意向量垂直条件的运用和中点坐标公式,考查构造法和函数的单调性运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①②⑤ | C. | ①④⑤ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
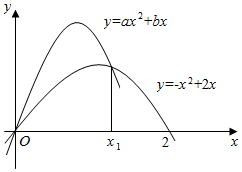 已知y=ax2+bx(a<0)通过点(1,2),且其图象与y=-x2+2x的图象有二个交点(如图所示).
已知y=ax2+bx(a<0)通过点(1,2),且其图象与y=-x2+2x的图象有二个交点(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2\sqrt{x}}}$ | B. | -$\frac{1}{{2\sqrt{x}}}$ | C. | -$\frac{{\sqrt{x}}}{2}$ | D. | $\frac{{\sqrt{x}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | {2} | C. | [0,2] | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com