
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (Ⅰ)关键分层抽样的特点计算x,y;
(Ⅱ)关键2×2列联表以及参考公式计算k2,与临界表比较多的答案;
(Ⅲ)利用条件概率公式解答.
解答 解:(Ⅰ) 从甲校抽取110×$\frac{600}{600+500}$=60(人),从乙校抽取110×$\frac{500}{500+600}$=50(人),故x=9,y=6.---------(2分)
| 甲校 | 乙校 | 总计 | |
| 优秀 | 15 | 20 | 35 |
| 非优秀 | 45 | 30 | 75 |
| 总计 | 60 | 50 | 110 |
点评 本题考查了随机抽样中的分层抽样以及独立检验思想;明确分层抽样的特点和独立检验思想是解答的关键.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
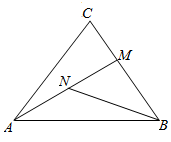 如图,在边长为1的正三角形ABC中,$\overrightarrow{BM}$=2$\overrightarrow{MC}$,N为AM的中点.
如图,在边长为1的正三角形ABC中,$\overrightarrow{BM}$=2$\overrightarrow{MC}$,N为AM的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{e}$) | B. | (0,$\frac{1}{e+1}$] | C. | (0,$\frac{1}{e}$] | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com