
分析 画出图形,利用几何概型公式,求出区域的面积比即可
解答  解:以(x,y)为坐标,满足0≤x≤1,0≤y≤1的是图中边长为1的正方形,面积为1,满足则不等式y≤2x的所有解如图阴影部分
解:以(x,y)为坐标,满足0≤x≤1,0≤y≤1的是图中边长为1的正方形,面积为1,满足则不等式y≤2x的所有解如图阴影部分
,面积为1-$\frac{1}{2}×1×\frac{1}{2}$=$\frac{3}{4}$,故概率是$\frac{\frac{3}{4}}{1}=\frac{3}{4}$;
故答案为:$\frac{3}{4}$.
点评 本题考查的知识点是几何概型,由题意,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=N(A)/N求解;本题所求概率是面积的比.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
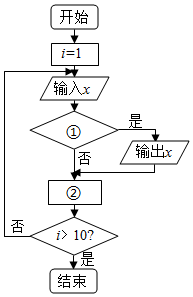 程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是( )
程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i-1 | B. | x<60?,i=i+1 | C. | x>60?,i=i+1 | D. | x<60?,i=i-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2x | B. | -3x | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
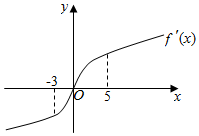
| A. | (-3,0) | B. | (-3,5) | C. | (0,5) | D. | (-∞,-3)∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①②⑤ | C. | ①④⑤ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com