
分析 (1)正项数列{an}满足an+1-a1=(a2-1)Sn(n∈N*),令n=1,得a2-a1=(a2-1)a1,因an>0,则a1=1,得$\frac{a_2}{a_1}={a_2}=t$,当n≥2 时,an+1-a1=(a2-1)Sn,an-a1=(a2-1)Sn-1,两式相减得:an+1=a2an,利用等比数列的通项公式即可得出.
(2)令${f_n}(t)={S_n}-\frac{{n({a_1}+{a_n})}}{2}=1+t+…+{t^{n-1}}-\frac{{n(1+{t^{n-1}})}}{2},t>0$.当t=1 时,fn(1)=0,即${S_n}=\frac{{n({a_1}+{a_n})}}{2}$.当t≠1 时,${f_n}'(t)=1+2t+…+(n-1){t^{n-2}}-\frac{{n(n-1){t^{n-2}}}}{2}$,利用导数研究其单调性即可得出.
解答 解:(1)正项数列{an}满足an+1-a1=(a2-1)Sn(n∈N*),令n=1,得a2-a1=(a2-1)a1,
即a2=a2•a1,因an>0,则a1=1,得$\frac{a_2}{a_1}={a_2}=t$,…(2分)
当n≥2 时,an+1-a1=(a2-1)Sn,an-a1=(a2-1)Sn-1,
两式相减得:an+1-an=(a2-1)an,即an+1=a2an,
因an>0,则$\frac{{{a_{n+1}}}}{a_n}={a_2}=t$ …(5分)
综上:$\frac{{{a_{n+1}}}}{a_n}=t(n∈N*)$ …(6分)
从而,{an} 是以1为首项,t 为公比的等比数列,
故${a_n}={t^{n-1}}$.…(7分)
(2)令${f_n}(t)={S_n}-\frac{{n({a_1}+{a_n})}}{2}=1+t+…+{t^{n-1}}-\frac{{n(1+{t^{n-1}})}}{2},t>0$.
当t=1 时,fn(1)=0,即${S_n}=\frac{{n({a_1}+{a_n})}}{2}$ …(9分)
当t≠1 时,${f_n}'(t)=1+2t+…+(n-1){t^{n-2}}-\frac{{n(n-1){t^{n-2}}}}{2}$,
若t∈(0,1),${f_n}'(t)>[1+2+…+(n-1)]{t^{n-2}}-\frac{{n(n-1){t^{n-2}}}}{2}=0$.
若t∈(1,+∞),${f_n}'(t)<[1+2+…+(n-1)]{t^{n-2}}-\frac{{n(n-1){t^{n-2}}}}{2}=0$,
即fn'(t) 在t∈(0,1)时单调递增,当t∈(1,+∞) 时单调递减,…(14分)
则fn(t)<fn(1)=0,即${S_n}<\frac{{n({a_1}+{a_n})}}{2}$,…(15分)
故${S_n}≤\frac{{n({a_1}+{a_n})}}{2}$,当且仅当t=1 时取“=”.…(16分)
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、利用导数研究函数的单调性极值最值,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
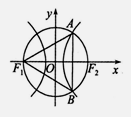 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016-1 | B. | 3•21008-3 | C. | 22009-3 | D. | 22010-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为5.
《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com