؟¼µم£؛ض±دكسëش²×¶اْدكµؤ×غ؛دختجâ
רجâ£؛¼ئثمجâ,ئ½أودٍء؟¼°س¦سأ,ض±دكسëش²,ش²×¶اْدكµؤ¶¨زه،¢ذشضتسë·½³ج
·ضخِ£؛£¨¢ٌ£©ةè³ِحضش²·½³ج£¬سةحضش²µؤ¶¨زه؟ةµأa£¬شظسةأو»¹«ت½£¬½ل؛دa£¬b£¬cµؤ¹طدµ£¬¼´؟ةµأµ½حضش²·½³ج£»
£¨¢ٍ£©ةèN£¨x£¬y£©£¬سةضطذؤ×ّ±ê¹«ت½£¬½ل؛ددٍء؟µؤتء؟»×ّ±ê¹«ت½£¬¼´؟ةµأµ½¹ى¼£·½³ج£»
£¨¢َ£©إذ¶د¶¯µمNµؤ¹ى¼££¬ةèP£¨m£¬n£©£¬شٍ¸ù¾فئ½أو¼¸؛خضھت¶µأµ½|
|=|
|£¬¼°cos£¼
£¬£¾£¬´س¶ّ¸ù¾فئ½أودٍء؟تء؟»µؤ¶¨زه¼°¾ùضµ²»µبت½µأ
•µؤ×îذ،ضµ£®
½â´ً£؛
½â£؛£¨¢ٌ£©سةجâزâةèحضش²µؤ·½³جخھ
+=1(a£¾b£¾0)£¬
زٍخھMتاحضش²¶جضلµؤز»¸ِ¶ثµم£¬¹F
1µؤض±دكlسëحضش²½»سعA£¬Bء½µم£¬
،÷MF
1F
2µؤأو»خھ4£¬،÷ABF
2µؤضـ³¤خھ
8£¬
ثùزش
4a=8£¬•b•2c=4£¬
،à
،àb=c=2£¬a=2£¬
ثùزش£¬ثùاَµؤحضش²·½³جخھ
+=1£®
£¨¢ٍ£©ةèN£¨x£¬y£©£¬شٍسة£¨¢ٌ£©µأF
1£¨-2£¬0£©£¬F
2£¨2£¬0£©£¬ثùزش
G(£¬)£¬
´س¶ّ
=(2-£¬-)£¬
=(x£¬y)£®زٍخھ
•=0£¬
ثùزشسذ
(2-£¬-)•(x£¬y)=(2-)x+(-)y=0£¬¼´x2+y2-6x=0£¬
سةسعGتا،÷NF
1F
2µؤضطذؤ£¬¼´N£¬F
1£¬F
2س¦µ±تاز»¸ِب½اذخµؤب¸ِ¶¥µم£¬
زٍ´ثثùاَ¶¯µمNµؤ¹ى¼£·½³جخھx
2+y
2-6x=0£¨y،ظ0£©£®
£¨¢َ£©سة£¨¢ٍ£©ضھ¶¯µمNµؤ¹ى¼£·½³جخھx
2+y
2-6x=0£¨y،ظ0£©£¬
¼´£¨x-3£©
2+y
2=9£¨y،ظ0£©£®
دشب»´ث¹ى¼£تازشµمC£¨3£¬0£©£©خھش²ذؤ£¬°ë¾¶r=3µؤش²
³ب¥ء½µم£¨0£¬0£©£¬£¨6£¬0£©ت£سà²؟·ضµؤ²؟·ضاْدك£®
ةèP£¨m£¬n£©£¬شٍ¸ù¾فئ½أو¼¸؛خضھت¶µأ|
|=|
|=
=
£¬
cos£¼
£¬£¾=cos2،دQPC=1-2sin
2،دQPC=1-2•£¨
£©
2=1-
£¬
´س¶ّ¸ù¾فئ½أودٍء؟تء؟»µؤ¶¨زه¼°¾ùضµ²»µبت½µأ£؛
•=|
|•|
|•cos£¼
£¬
£¾=[£¨m-3£©
2+n
2-9]•[1-
]
=[£¨m-3£©
2+n
2]+
-27،ف2
-27=18
-27£®
µ±از½ِµ±
(m-3)2+n2=9ت±£¬ب،،°=،±£¨،ù£©
سةµمP£¨m£¬n£©شعحضش²
+=1ةد£¨·ا¶جضل¶ثµم£©£¬²¢ازشعش²£¨x-3£©
2+y
2=9ح⣬
؟ةضھ
3£¼||،ـ3+2µ«||،ظ||=⇒(m-3)2+n2،ت(9£¬13)،ب(13£¬17+12]سةسع
9،ت(9£¬13)£¬ثùزشجُ¼£¨،ù£©µؤزھاَآْ×م£®
زٍ´ث
•µؤ×îذ،ضµخھ
18-27£®
µمئہ£؛±¾جâ؟¼²éحضش²µؤ¶¨زه،¢·½³ج؛حذشضت£¬؟¼²é¹ى¼£·½³جµؤاَ·¨£¬؟¼²éئ½أودٍء؟µؤتء؟»µؤ¶¨زه؛حذشضت£¬؟¼²éض±دك؛حش²µؤخ»ضأ¹طدµ£¬تôسعضذµµج⣮



 شؤ¶ء؟ى³µدµءذ´ً°¸
شؤ¶ء؟ى³µدµءذ´ً°¸
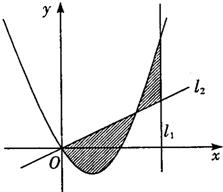 زرضھ¶´خ؛¯تf£¨x£©=3x2-3x£¬ض±دكl1£؛x=2؛حl2£؛y=3tx£¨ئنضذtخھ³£ت£¬از0£¼t£¼1£©£¬ض±دكl2سë؛¯تf£¨x£©µؤح¼دَزش¼°ض±دكl1،¢l2سë؛¯تf£¨x£©µؤح¼دَثùخ§³ةµؤ·â±صح¼ذخبçح¼ضذزُس°ثùت¾£¬ةèصâء½¸ِزُس°اّسٍµؤأو»ض®؛حخھS£¨t£©£®
زرضھ¶´خ؛¯تf£¨x£©=3x2-3x£¬ض±دكl1£؛x=2؛حl2£؛y=3tx£¨ئنضذtخھ³£ت£¬از0£¼t£¼1£©£¬ض±دكl2سë؛¯تf£¨x£©µؤح¼دَزش¼°ض±دكl1،¢l2سë؛¯تf£¨x£©µؤح¼دَثùخ§³ةµؤ·â±صح¼ذخبçح¼ضذزُس°ثùت¾£¬ةèصâء½¸ِزُس°اّسٍµؤأو»ض®؛حخھS£¨t£©£® بçح¼£¬ثؤہâ׶P-ABCDµؤµ×أوABCDتا¾طذخ£¬²àأوPABتاصب½اذخ£¬AB=2£¬BC=
بçح¼£¬ثؤہâ׶P-ABCDµؤµ×أوABCDتا¾طذخ£¬²àأوPABتاصب½اذخ£¬AB=2£¬BC=