
| A. | (-∞,4] | B. | (6,+∞) | C. | (4,6) | D. | [4,6] |
分析 根据题意,得出圆C的圆心C与半径r,设点P(a,b)在圆C上,表示出$\overrightarrow{AP}$=(a+m,b),$\overrightarrow{BP}$=(a-m,b),利用$\overrightarrow{PA}•\overrightarrow{PB}=0$,求出m2,根据|OP|表示的几何意义,得出m的取值范围.
解答 解:∵圆C:(x-3)2+(y-4)2=1,
∴圆心C(3,4),半径r=1;
设点P(a,b)在圆C上,则$\overrightarrow{AP}$=(a+m,b),$\overrightarrow{BP}$=(a-m,b);
∵$\overrightarrow{PA}•\overrightarrow{PB}=0$
∴(a+m)(a-m)+b2=0;
即m2=a2+b2;
∴|OP|=$\sqrt{{a}^{2}+{b}^{2}}$,
∴|OP|的最大值是|OC|+r=5+1=6,最小值是|OC|-r=5-1=4;
∴m的取值范围是[4,6].
故选D.
点评 本题考查了平面向量的应用问题,也考查了直线与圆的应用问题,是综合性题目.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 9π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{17}}{3}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
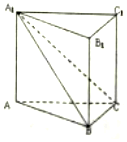 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
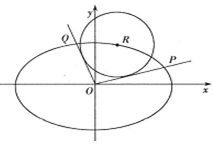 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △PF1F2的内切圆圆心在直线$x=\frac{a}{2}$上 | B. | △PF1F2的内切圆圆心在直线x=b上 | ||
| C. | △PF1F2的内切圆圆心在直线OP上 | D. | △PF1F2的内切圆经过点(a,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com