
| A. | 4π | B. | 8π | C. | 9π | D. | 36π |
分析 由余弦定理化简已知等式可求c的值,利用同角三角函数基本关系式可求sinC的值,进而利用正弦定理可求三角形的外接圆的半径R的值,利用圆的面积公式即可计算得解.
解答 解:∵bcosA+acosB=2,
∴由余弦定理可得:b×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$+a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=2,整理解得:c=2,
又∵$cosC=\frac{{2\sqrt{2}}}{3}$,可得:sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{1}{3}$,
∴设三角形的外接圆的半径为R,则2R=$\frac{c}{sinC}$=$\frac{2}{\frac{1}{3}}$=6,可得:R=3,
∴△ABC的外接圆的面积S=πR2=9π.
故选:C.
点评 本题主要考查了余弦定理,同角三角函数基本关系式,正弦定理,圆的面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
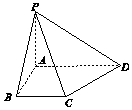 四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )| A. | $\frac{\sqrt{42}}{7}$ | B. | $\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
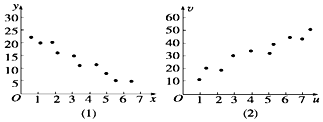 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y正相关,u与v负相关 | ||
| C. | 变量x与y负相关,u与v正相关 | D. | 变量x与y负相关,u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
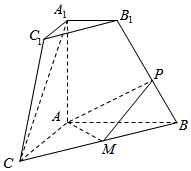 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (6,+∞) | C. | (4,6) | D. | [4,6] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com