
分析 (1)设P(x,y),则由垂径定理能求出曲线C的方程.
(2)设直线AB:y=kx+m(k≠0),联立方程y2=4x,得ky2-4y+4m=0,由此利用根的判别式、韦达定理、线段中点坐标坐标公式、弦长公式,由此能求出△ABQ的面积的最大值为8,此时直线AB的方程为y=±x.
解答 解:(1)设P(x,y),则由垂径定理得$\sqrt{{{(x-2)}^2}+{y^2}}=\sqrt{{{|x|}^2}+{2^2}}$,
化简得y2=4x,
所以曲线C的方程是:y2=4x. …(4分)
(2)依题意可知直线AB的斜率存在且不为零,
所以设直线AB:y=kx+m(k≠0),
并联立方程y2=4x消x得ky2-4y+4m=0,
因为△>0⇒mk<1①,且${y_1}+{y_2}=\frac{4}{k}$,②${y_1}{y_2}=\frac{4m}{k}$,③,
又y1+y2=k(x1+x2)+2m=4k+2m=$\frac{4}{k}$,由此得$m=\frac{2}{k}-2k$④,
把④代入①得${k^2}>\frac{1}{2}$⑥…(6分)
设线段AB的中点为M,则M(2,$\frac{2}{k})$,则直线l:$y=-\frac{1}{k}(x-2)+\frac{2}{k}$,
令y=0⇒x=4⇒Q(4,0),…(8分)
设直线AB与x轴相交于点D,则$D(-\frac{m}{k}$,0),
所以${S_{△ABQ}}=\frac{1}{2}|{4+\frac{m}{k}}||{{y_1}-{y_2}}|$=$\frac{1}{2}|{4+\frac{m}{k}}|\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$⑤
把②③④代入⑤化简得S△ABQ=$4(1+\frac{1}{k^2})\sqrt{2-\frac{1}{k^2}}$,…(10分)
设$\sqrt{2-\frac{1}{k^2}}$=t,由⑥知 t>0,且 $\frac{1}{k^2}=2-{t^2}$,
S△ABQ=12t-4t3,令f(t)=12t-4t3,f'(t)=12-12t2=12(1-t)(1+t),
当0<t<1时,f'(t)>0,当t>1时,f'(t)<0,所以当t=1时,此时k=±1,
函数f(t)的最大值为f(1)=8,因此△ABQ的面积的最大值为8,
此时直线AB的方程为y=±x. …(12分)
点评 本题考查曲线方程的求法,考查三角形面积的最大值的求法,考查直线方程的求法,考查推理论证能力、运算求解能力,考查转化化归思想、整体思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
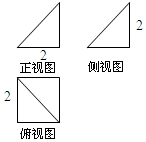
| A. | 4 | B. | $\frac{7}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{6}$ | B. | $\frac{20}{6}$ | C. | $\frac{23}{6}$ | D. | $\frac{26}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若¬p:?x∈R,x2+x+1≥0 | B. | p为假命题 | ||
| C. | p∨¬p为假命题 | D. | ¬p为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com