
分析 (1)设出直线AB的方程,代入抛物线的方程,运用韦达定理和点满足直线方程,由向量的数量积的坐标表示,化简即可得到所求值;
(2)求得切线的斜率和切线的方程,运用弦长公式,可得|AB|,|CD|,求得四边形ABCD的面积,运用对勾函数的性质,解方程可得k的值.
解答 解:(1)设直线AB方程为$y=kx+\frac{p}{2},A({x_1},{y_1}),B({x_2},{y_2})$,
联立直线AB与抛物线方程
$\left\{\begin{array}{l}{y=kx+\frac{p}{2}}\\{{x}^{2}=2py}\end{array}\right.$,得x2-2pkx-p2=0,
则x1+x2=2pk,x1x2=-p2,
可得$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=x1x2=x1x2+(kx1+$\frac{p}{2}$)(kx2+$\frac{p}{2}$)
=(1+k2)x1x2+$\frac{{p}^{2}}{4}$+$\frac{pk}{2}$(x1+x2)
=(1+k2)(-p2)+$\frac{{p}^{2}}{4}$+$\frac{pk}{2}$•2pk=-$\frac{3}{4}$p2;
(2)由x2=2py,知$y'=\frac{x}{p}$,
可得曲线在A,B两点处的切线的斜率分别为$\frac{x_1}{p},\frac{x_2}{p}$,
即有AM的方程为$y-{y_1}=\frac{x_1}{p}(x-{x_1})$,BM的方程为$y-{y_2}=\frac{x_2}{p}(x-{x_2})$,
解得交点$M(pk,-\frac{p}{2})$,
则${k_{MF}}=-\frac{1}{k}$,知直线MF与AB相互垂直.
由弦长公式知,|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{4{p}^{2}{k}^{2}+4{p}^{2}}$=2p(1+k2),
用$-\frac{1}{k}$代k得,$\left|{CD}\right|=2p(\frac{1}{k^2}+1)$,
四边形ACBD的面积$S=2{p^2}(2+{k^2}+\frac{1}{k^2})=\frac{32}{3}{p^2}$,
依题意,得${k^2}+\frac{1}{k^2}$的最小值为$\frac{10}{3}$,
根据$f(x)=x+\frac{1}{x}\;(x>0)$的图象和性质得,k2=3或${k^2}=\frac{1}{3}$,
即$k=±\sqrt{3}$或$k=±\frac{{\sqrt{3}}}{3}$.
点评 本题考查直线与抛物线的位置关系,主要是相切的条件,考查直线方程和抛物线方程联立,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | x2+y2=8 | B. | x2+y2=64 | C. | x2+y2=36 | D. | x2+y2=6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
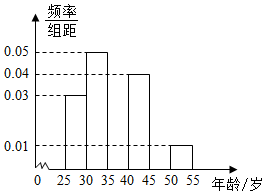
| 组别 | 分组 | 高收入的人数 | 高收入人数占本组的比例 |
| 第一组 | [25,30) | 18 | 0.12 |
| 第二组 | [30,35) | 36 | 0.144 |
| 第三组 | [35,40) | 48 | 0.192 |
| 第四组 | [40,45) | A | 0.15 |
| 第五组 | [45,50) | 12 | b |
| 第六组 | [50,55) | 6 | 0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{ω}$ | C. | $\frac{π}{2ω}$ | D. | 与a有关的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com