Question

11．中国经济的高速增长带动了居民收入的提高，为了调查高收入（年收入是当地人均年收入10倍以上）人群的年龄分布情况，某校学生利用暑假进行社会实践，对年龄在[25，55）内的人群随机调查了1000人的收入情况，根据调查结果和收集的数据得到如下统计表和各年龄段人数的频率分布直方图．

组别	分组	高收入的人数	高收入人数占本组的比例
第一组	[25，30）	18	0.12
第二组	[30，35）	36	0.144
第三组	[35，40）	48	0.192
第四组	[40，45）	A	0.15
第五组	[45，50）	12	b
第六组	[50，55）	6	0.12

（1）补全频率分布直方图，根据频率分布直方图，求这1000人年龄的中位数；
（2）求统计表中a，b的值，为了分析高收入居民人数与年龄的关系，要从高收入人群中按年龄组用分层抽样的方法抽取25人作进一步分析，则年龄在[30，40）内的高收入人群应抽取多少人？

Answer 1

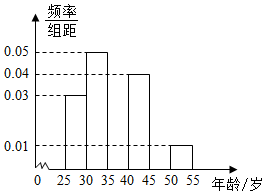
分析 （1）计算每一组内的人数，频率值，求出第三组[35，40）、第五组[45，50）内的频率，补全频率分布直方图，根据频率分布直方图，计算中位数；
（2）计算出A、b的值，再根据分层抽样方法计算抽取25时在[30，40）内应抽取的人数．

解答 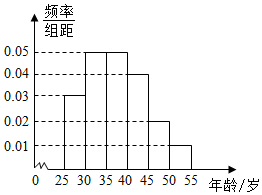解：（1）第一组[25，30）内的人数是$\frac{18}{0.12}$=150，频率为0.03×5=0.15；
第二组[30，35）内的人数是$\frac{36}{0.144}$=250，频率为0.05×5=0.25；
第三组[35，40）内的人数是$\frac{48}{0.192}$=250，频率为0.05×5=0.25；
第四组[40，45）内的频率为0.04×5=0.2，频数是1000×0.2=200，对应高收入人数是A=200×0.15=30；
第五组[45，50）内的频率为1-（0.03+0.05+0.05+0.04+0.01）×5=0.1，频数为1000×0.1=100，高收入人数占本组的比例为b=$\frac{12}{100}$=0.12；
补全频率分布直方图，如图所示；
根据频率分布直方图，得；
0.03×5+0.05×5=0.4＜0.5，
所以中位数在[35，40）内，设为x，
则0.4+（x-35）×0.05=0.5，
解得x=37，
所以这1000人年龄的中位数为37；
（2）由（1）知，A=30，b=0.12，
高收入人数为18+36+48+30+12+6=150，
用分层抽样的方法抽取25人，
则年龄在[30，40）内的高收入人群应抽取25×$\frac{36+48}{150}$=14人．

点评 本题考查了频率分布直方图的应用问题，也考查了分层抽样方法的应用问题，是基础题目．