
分析 利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=g(x)=-1+ax,
则y=logat,
∵a>0且a≠1,
∴t=g(x)=-1+ax在[2,4]上是增函数,
∴要使函数y=loga(-1+ax)在[2,4]上是减函数,
则y=logat,为减函数,且g(2)>0,
则$\left\{\begin{array}{l}{0<a<1}\\{-1+2a>0}\end{array}\right.$,得$\left\{\begin{array}{l}{0<a<1}\\{a>\frac{1}{2}}\end{array}\right.$,
即$\frac{1}{2}$<a<1,
即实数a的取值范围是($\frac{1}{2}$,1),
故答案为:($\frac{1}{2}$,1)
点评 本题主要考查函数单调性的应用,利用换元法结合复合函数单调性之间的关系进行转化是解决本题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,lg6] | B. | (-∞,3lg2] | C. | [lg6,+∞) | D. | [3lg2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=8 | B. | x2+y2=64 | C. | x2+y2=36 | D. | x2+y2=6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 3$\sqrt{2}$ | C. | 36-16$\sqrt{2}$ | D. | 4$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
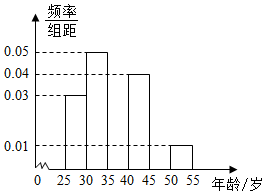
| 组别 | 分组 | 高收入的人数 | 高收入人数占本组的比例 |
| 第一组 | [25,30) | 18 | 0.12 |
| 第二组 | [30,35) | 36 | 0.144 |
| 第三组 | [35,40) | 48 | 0.192 |
| 第四组 | [40,45) | A | 0.15 |
| 第五组 | [45,50) | 12 | b |
| 第六组 | [50,55) | 6 | 0.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com