
分析 (Ⅰ)设|PF1|=m,|PF2|=n,由椭圆定义得m+n=2a,设椭圆的半焦距为c,则a2=b2+c2,再利用余弦定理、三角形面积计算公式即可得出.
(II)可得椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.当AB,AC中一个斜率为零,一个斜率不存在显然不符合题意.设AB:y=kx+1,不妨设k>0.联立直线AB和椭圆方程得(4k2+1)x2+8kx=0,可得|AB|,由AB⊥AC,得kAB•kAC=-1,可得|AC|,利用|AB|=|AC|,解出即可得出.
解答 解:(Ⅰ)设|PF1|=m,|PF2|=n,由椭圆定义得m+n=2a,
设椭圆的半焦距为c,则a2=b2+c2,
对△PF1F2由余弦定理得${(2c)^2}={m^2}+{n^2}-2mncos∠{F_1}P{F_2}={(m+n)^2}-3mn={(2a)^2}-3mn$,
解得$mn=\frac{4}{3}{b^2}$,
又${S_{△P{F_1}{F_2}}}=\frac{1}{2}mnsin{60°}=\frac{{\sqrt{3}}}{3}{b^2}$,结合${S_{△P{F_1}{F_2}}}=\frac{{\sqrt{3}}}{3}$得b=1.
(Ⅱ)可得椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
当AB,AC中一个斜率为零,一个斜率不存在显然不符合题意
设AB:y=kx+1,不妨设k>0.
联立直线AB和椭圆方程得(4k2+1)x2+8kx=0,
解得两根为${x_1}=0,{x_2}=-\frac{8k}{{4{k^2}+1}}$.
∴$|AB|=\sqrt{1+{k^2}}|\frac{8k}{{4{k^2}+1}}|$,由AB⊥AC,得kAB•kAC=-1,
把|AB|中的k换成$-\frac{1}{k}$,可得$|AC|=\sqrt{1+\frac{1}{k^2}}|\frac{{-8\frac{1}{k}}}{{4\frac{1}{k^2}+1}}|=\frac{{8\sqrt{{k^2}+1}}}{{4+{k^2}}}$,
由|AB|=|AC|,得$\sqrt{1+{k^2}}|\frac{8k}{{4{k^2}+1}}|=\frac{{8\sqrt{{k^2}+1}}}{{4+{k^2}}}$,结合k>0化简得k3-4k2+4k-1=0,整理得(k-1)(k2-3k+1)=0,
解得${k_1}=1,{k_2}=\frac{{3+\sqrt{5}}}{2},{k_3}=\frac{{3-\sqrt{5}}}{2}$,均符合k>0,
所以符合条件的△ABC的个数有3个.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、余弦定理、相互垂直的直线斜率之间的关系、等腰三角形的性质,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,lg6] | B. | (-∞,3lg2] | C. | [lg6,+∞) | D. | [3lg2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 90 | C. | 150 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=8 | B. | x2+y2=64 | C. | x2+y2=36 | D. | x2+y2=6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
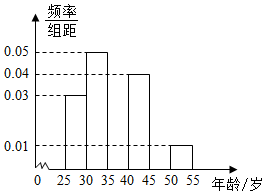
| 组别 | 分组 | 高收入的人数 | 高收入人数占本组的比例 |
| 第一组 | [25,30) | 18 | 0.12 |
| 第二组 | [30,35) | 36 | 0.144 |
| 第三组 | [35,40) | 48 | 0.192 |
| 第四组 | [40,45) | A | 0.15 |
| 第五组 | [45,50) | 12 | b |
| 第六组 | [50,55) | 6 | 0.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com