
| A. | (-∞,-1]∪[4,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,0]∪[3,4] | D. | (-∞,0]∪[3,+∞) |
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
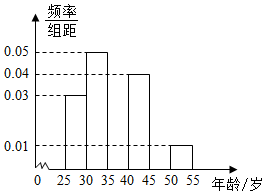
| 组别 | 分组 | 高收入的人数 | 高收入人数占本组的比例 |
| 第一组 | [25,30) | 18 | 0.12 |
| 第二组 | [30,35) | 36 | 0.144 |
| 第三组 | [35,40) | 48 | 0.192 |
| 第四组 | [40,45) | A | 0.15 |
| 第五组 | [45,50) | 12 | b |
| 第六组 | [50,55) | 6 | 0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,已知点S(0,3),SA,SB与圆C:x2+y2-my=0(m>0)和抛物线x2=-2py(p>0)都相切,切点分别为M,N和A,B,SA∥ON,则点A到抛物线准线的距离为( )
如图所示,已知点S(0,3),SA,SB与圆C:x2+y2-my=0(m>0)和抛物线x2=-2py(p>0)都相切,切点分别为M,N和A,B,SA∥ON,则点A到抛物线准线的距离为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{ω}$ | C. | $\frac{π}{2ω}$ | D. | 与a有关的值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com