
| A. | 8小时 | B. | 9小时 | C. | 10小时 | D. | 12小时 |
分析 由已知得AO=OD=400,OA⊥OD,OB=OC=300,∠OAB=45°,由余弦定理求出AB=CD=200$\sqrt{2}-100$,由此能求出这个台风对码头产生影响的时间.
解答 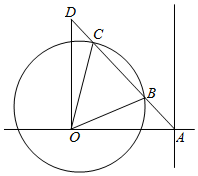 解:如图,由已知得AO=OD=400,
解:如图,由已知得AO=OD=400,
OA⊥OD,
OB=OC=300,∠OAB=45°,
设CD=AB=x,
则90000=160000+x2-800x×$\frac{\sqrt{2}}{2}$,
解得AB=CD=200$\sqrt{2}-100$,
∴BC=$\sqrt{160000+160000}$-2(200$\sqrt{2}$-100)
=200,
由题意当台风中心位于BC线段上时,
将对码头O产生影响,
∵台风中心正以每小时20公里的速度向西北方向移动,
∴这个台风对码头产生影响的时间为:$\frac{200}{20}=10$小时.
故选:C.
点评 本题考查圆的知识在生产生活中的应用,是中档题,解题时要认真审题,注意余弦定理和数形结合思想的合理运用.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{27}{32}$ | B. | $\frac{3}{4}$ | C. | -$\frac{17}{32}$ | D. | $\frac{17}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
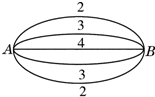 如图所示,A,B两点5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P(ξ≥8)=$\frac{4}{5}$.
如图所示,A,B两点5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P(ξ≥8)=$\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示:
某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y═-sinx | C. | y=2x+1 | D. | y=cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com