
分析 (1)由题意得,定义域为R即|x+2|+|6-x|-m≥0恒成立,所以利用不等变换求出|x+2|+|6-x|的最小值,即可求出m的范围;
(2)由(10可知n=mmax,求出a,b的关系式,化简求出2a+$\frac{3}{2}$b的最小值.
解答 解:(1)由题意,得|x+2|+|6-x|-m≥0在R上恒成立,即m≤|x+2|+|6-x|恒成立.
因为|x+2|+|6-x|≥|(x+2)+(6-x)|=8(当且仅当(x+2)(6-x)≥0即-2≤x≤6时等号成立),
所以m∈(-∞,8];
(2)由(1)知n=8,
所以$\frac{8}{3a+b}+\frac{2}{a+2b}=8$,
$2a+\frac{3}{2}b=\frac{1}{2}[{({3a+b})+({a+2b})}]=\frac{1}{16}[{({3a+b})+({a+2b})}](\frac{8}{3a+b}+\frac{2}{a+2b})$$≥\frac{1}{16}{(\sqrt{3a+b}•\sqrt{\frac{8}{3a+b}}+\sqrt{a+2b}•\sqrt{\frac{2}{a+2b}})^2}=\frac{1}{16}(3\sqrt{2}{)^2}=\frac{9}{8}$
(当且仅当$\left\{{\begin{array}{l}{a=3b}\\{\frac{8}{3a+b}+\frac{2}{a+2b}=8}\end{array}}\right.即\left\{{\begin{array}{l}{a=\frac{9}{20}}\\{b=\frac{3}{20}}\end{array}}\right.时等号成立$),
所以$2a+\frac{3}{2}b$的最小值是$\frac{9}{8}$.
点评 本题主要考察含绝对值不等式与基本等式,解题关键是将题目转化为恒成立问题,以及变形为柯西不等式形式,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8小时 | B. | 9小时 | C. | 10小时 | D. | 12小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
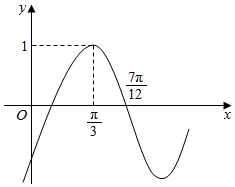 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如下结论中正确的是( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如下结论中正确的是( )| A. | f(x)图象C关于直线x=$\frac{11}{12}$π对称 | |
| B. | f(x)图象C关于点($\frac{2π}{3}$,0)对称 | |
| C. | 函数f(x)在区间($\frac{5π}{6}$,$\frac{4π}{3}$)内是增函数 | |
| D. | 把y=sin2x向右平移$\frac{π}{3}$个单位可以得到f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos100° | B. | sin100° | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com