
分析 (1)求得f(x)的导数,由切线的方程可得f(1)=2,f′(1)=1,解方程可得a,b,进而得到f(x)的解析式;
(2)求得g(x)=m[f(x)-x2+3lnx]+x2=x2+m(x+lnx)
①讨论当m=0,m>0,m<0,结合条件,运用参数分离,构造函数求得导数,运用单调性,可得m的范围;
②由①知,当m=-1时,g(x)=x2+m(x+lnx)≥0在x2-x≥lnx上恒成立,即x2-x≥lnx在$\frac{lnx}{x}≤x-1$上恒成立,即$\frac{lnx}{x}≤x-1$,分别令x=2,3,…,n-1,累加,结合对数的运算性质,即可得证.
解答 解:(1)f(x)=x2+2ax+blnx,导数$f'(x)=2x+2a+\frac{b}{x}$,
可得$\left\{\begin{array}{l}f'(1)=1\\ f(1)=2\end{array}\right.$,即$\left\{\begin{array}{l}2a+b+2=1\\ 1+2a=2\end{array}\right.$,
解得$\left\{\begin{array}{l}a=\frac{1}{2}\\ b=-2\end{array}\right.$,
则f(x)=x2+x-2lnx;
(2)g(x)=m[f(x)-x2+3lnx]+x2=x2+m(x+lnx)
①当m=0时,g(x)=x2,因为x>0,g(x)=x2>0满足题意;
当m>0时,x∈(0,1)时,lnx<0,mlnx<0,
从而“?x>0,g(x)=x2+m(x+lnx)>0”不成立;
当m<0时,由g(x)=x2+m(x+lnx)>0,得$\frac{1}{m}<-(\frac{1}{x}+\frac{lnx}{x^2})$,
设$h(x)=-(\frac{1}{x}+\frac{lnx}{x^2})$,则$h'(x)=\frac{x-1}{x^3}+\frac{2lnx}{x^3}$,当x=1时,h'(x)=0,
则当0<x<1时,h'(x)<0,h(x)在x>1上递减,
当x>1时,h'(x)>0,h(x)在h(x)≥h(1)=-1上递增,
所以h(x)≥h(1)=-1,即$\frac{1}{m}<-1$,所以-1<m<0
综上所述,实数m的取值范围是-1<m≤0;
②由①知,当m=-1时,g(x)=x2+m(x+lnx)≥0在x2-x≥lnx上恒成立,
即x2-x≥lnx在$\frac{lnx}{x}≤x-1$上恒成立,即$\frac{lnx}{x}≤x-1$,
当且仅当$\frac{ln2}{2}<1,\frac{ln3}{3}<2,\frac{ln4}{4}<3,…\frac{lnn}{n}<n-1$时等号成立.
所以有$\frac{ln2}{2}<1,\frac{ln3}{3}<2,\frac{ln4}{4}<3,…\frac{lnn}{n}<n-1$,
叠加得$\frac{ln2}{2}+\frac{ln3}{3}+\frac{ln4}{4}+…+\frac{lnn}{n}<1+2+3+…+(n-1)=\frac{n(n-1)}{2}$,
即$\frac{ln2}{2}+\frac{ln3}{3}+\frac{ln4}{4}+…+\frac{lnn}{n}<\frac{n(n-1)}{2}$
可得$ln(\sqrt{2}•\root{3}{3}•\root{4}{4}•\root{5}{5}…\root{n}{n})<\frac{n(n-1)}{2}$
所以$\sqrt{2}•\root{3}{3}•\root{4}{4}•\root{5}{5}…\root{n}{n}<{e^{\frac{n(n-1)}{2}}}$得证.
点评 本题考查导数的运用:求切线的方程和单调性,考查分类讨论的思想方法和综合法证明不等式的方法,注意运用累加法和对数的性质,本题也可运用数学归纳法证明,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
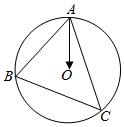
| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com