练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某年级480名学生在一次面米测试中，成绩全部介于13秒和18秒之间，将测试结果分成5组，如图为其频率分布直方图，如果从左到右的5个小矩形的面积之比为1：3：7：6：3，那么成绩在[16，18]的学生人数是216．

    分析 先求出成绩在[16，18]的学生的频率，由此能求出成绩在[16，18]的学生人数．

    解答 解：频率分布直方图中，
    从左到右的5个小矩形的面积之比为1：3：7：6：3，
    ∴成绩在[16，18]的学生的频率为：$\frac{6+3}{1+3+7+6+3}$=0.45，
    ∴成绩在[16，18]的学生人数是：480×0.45=216．
    故答案为：216．

    点评 本题考查频数的求法，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．已知曲线y=lnx的切线过原点，则此切线的斜率是$\frac{1}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

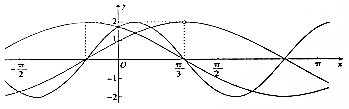    3．已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（　　）
    A．x=$\frac{π}{6}$B．x=$\frac{13π}{6}$C．x=-$\frac{23π}{12}$D．x=-$\frac{29π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=2lnx+ax-$\frac{4f′（2）}{x}$（a∈R）在x=2处的切线经过点（-4，2ln2）
    （1）讨论函数f（x）的单调性
    （2）若不等式$\frac{2xlnx}{{1-{x^2}}}＞mx-1$恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，以F1F2为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（　　）
    A．$\frac{x^2}{16}-\frac{y^2}{9}=1$B．$\frac{x^2}{3}-\frac{y^2}{4}=1$C．$\frac{x^2}{9}-\frac{y^2}{16}=1$D．$\frac{x^2}{4}-\frac{y^2}{3}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若两平面互相平行，第三个平面与这两个平面分别相交于l1，l2，则这两条直线之间的位置关系是平行（填写“平行、相交、异面”中的某一种或者某几种）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．用反证法证明：当m为任何实数时，关于x的方程x2-5x+m=0与2x2+x+6-m=0至少有一个方程有实数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设数列{an}的前n项和为Sn，已知a1=1，Sn=nan-n（n-1）（n=1，2，3，…）．
    （1）求数列{an}的通项公式；
    （2）若数列$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$前n项和为Tn，问满足${T_n}＞\frac{100}{209}$的最小正整数n是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若经过抛物线y2=4x焦点的直线l与圆（x-4）2+y2=4相切，则直线l的斜率为±$\frac{2\sqrt{5}}{5}$．

    查看答案和解析>>

    同步练习册答案