
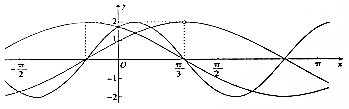
 已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )
已知ω>0,a>0,f(x)=asinωx+$\sqrt{3}$acosωx,g(x)=2cos(ax+$\frac{π}{6}$),h(x)=$\frac{f(x)}{g(x)}$这3个函数在同一直角坐标系中的部分图象如图所示,则函数g(x)+h(x)的图象的一条对称轴方程可以为( )| A. | x=$\frac{π}{6}$ | B. | x=$\frac{13π}{6}$ | C. | x=-$\frac{23π}{12}$ | D. | x=-$\frac{29π}{12}$ |
分析 由函数图象可知,三函数的最大值均为2,可得:a=1,由图象可知,f(x)的周期为π,可得ω=2,即可求出f(x)和g(x)解析式,因为h(x)=$\frac{f(x)}{g(x)}$可求h(x),那么函数g(x)+h(x)化解.可得对称轴方程.从而得答案.
解答 解:∵f(x)=asinωx+$\sqrt{3}$acosωx=2asin(ωx+$\frac{π}{3}$),g(x)=2cos(ax+$\frac{π}{6}$),
又由函数图象可知,三函数的最大值均为2,可得:a=1,
∴f(x)=2sin(ωx+$\frac{π}{3}$),g(x)=2cos(x+$\frac{π}{6}$),
由图象可知,f(x)的周期为π,∴ω=2
h(x)=$\frac{f(x)}{g(x)}$=$\frac{2sin(2x+\frac{π}{3})}{2cos(x+\frac{π}{6})}$=2sin(x+$\frac{π}{6}$),
那么函数g(x)+h(x)=2cos(x+$\frac{π}{6}$)+2sin(x+$\frac{π}{6}$)=$2\sqrt{2}$sin(x+$\frac{π}{6}$$+\frac{π}{4}$)=2$\sqrt{2}$sin(x$+\frac{5π}{12}$).
令x$+\frac{5π}{12}$=$\frac{π}{2}+kπ$,(k∈Z)
可得对称轴方程为x=$\frac{π}{12}+kπ$,
当k=-2时,可得x=-$\frac{23π}{12}$.
故选C.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用函数图象求出f(x)和g(x)解析式是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{7π}{12}$,$\frac{13π}{12}$) | B. | [$\frac{π}{2}$,π) | C. | [$\frac{π}{6}$,$\frac{π}{2}$) | D. | [$\frac{π}{6}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | cos10° | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {3} | C. | {2,3,4} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.
某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com