
分析 (1)利用已知条件转化为数列是等差数列,然后求解通项公式.
(2)化简数列的通项公式,利用裂项消项法求解即可.
解答 解:(1)当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1-2(n-1),
得an-an-1=2(n=2,3,4,…).
∴数列{an}是以a1=1为首项,2为公差的等差数列.故an=2n-1.-------(6分)
(2)${T_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{n-1}}{a_n}}}$=$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{{({2n-1})({2n+1})}}$=$\frac{1}{2}[(\frac{1}{1}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}({1-\frac{1}{2n+1}})$=$\frac{n}{2n+1}$-------(10分)
由${T_n}=\frac{n}{2n+1}>\frac{100}{209}$,得$n>\frac{100}{9}$,
满足${T_n}>\frac{100}{209}$的最小正整数为12.-------(12分)
点评 本题考查数列的递推关系式的应用,数列求和,考查计算能力.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | cos10° | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.
某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<$\frac{1}{3}$ | B. | $\frac{1}{3}$<a<$\frac{2}{3}$ | C. | a>1 | D. | $\frac{1}{3}$<a<$\frac{2}{3}$或a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
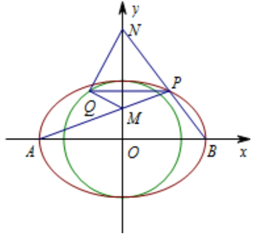 已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.
已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com