
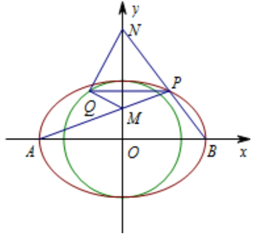
 已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.
已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.分析 (1)由题意可得a=2,b=c,b2+c2=a2,解方程可得b,c,进而得到圆O的方程和椭圆的离心率;
(2)设P(x0,y0)(y0≠0),Q(xQ,y0),分别代入圆和椭圆方程,运用直线方程的点斜式求得AP,BP的方程,令x=0,可得M,N的坐标,求得向量MQ,NQ的坐标,由向量垂直的条件:数量积为0,化简整理,即可得到结论.
解答  解:(1)由椭圆方程可得a=2,
解:(1)由椭圆方程可得a=2,
又以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,
可得b=c且b2+c2=a2,
解得a=2,b=c=$\sqrt{2}$,
则圆O的方程为x2+y2=2,椭圆C的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
(2)如图所示,设P(x0,y0)(y0≠0),Q(xQ,y0),
则$\left\{\begin{array}{l}\frac{{{x_0}^2}}{4}+\frac{{{y_0}^2}}{2}=1\\{x_Q}^2+{y_0}^2=2\end{array}\right.$即$\left\{\begin{array}{l}{x_0}^2=4-2{y_0}^2\\{x_Q}^2=2-{y_0}^2\end{array}\right.$,
又A(-2,0),B(2,0),由AP:$y=\frac{y_0}{{{x_0}+2}}(x+2)$,得$M(0,\frac{{2{y_0}}}{{{x_0}+2}})$.
由BP:$y=\frac{y_0}{{{x_0}-2}}(x-2)$,得$N(0,-\frac{{2{y_0}}}{{{x_0}-2}})$.
所以$\overrightarrow{QM}=(-{x_Q},\frac{{2{y_0}}}{{{x_0}+2}}-{y_0})$=$(-{x_Q},-\frac{{{x_0}{y_0}}}{{{x_0}+2}})$,
$\overrightarrow{QN}=(-{x_Q},-\frac{{2{y_0}}}{{{x_0}-2}}-{y_0})=(-{x_Q},-\frac{{{x_0}{y_0}}}{{{x_0}-2}})$,
所以$\overrightarrow{QM}•\overrightarrow{QN}={x_Q}^2+\frac{{{x_0}^2{y_0}^2}}{{{x_0}^2-4}}=2-{y_0}^2+\frac{{(4-2{y_0}^2){y_0}^2}}{{-2{y_0}^2}}=0$,
所以QM⊥QN,即MQ与NQ所在的直线互相垂直.
点评 本题考查椭圆的方程和性质,主要是离心率的求法,考查两直线垂直的条件,转化为两向量垂直的条件:数量积为0是解题的关键,考查直线和圆方程的运用,以及化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
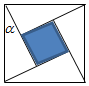 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是| A. | $1-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{4-\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{4}{3}}]$ | B. | $({\frac{4}{3},\frac{7}{3}}]$ | C. | $({\frac{7}{3},\frac{10}{3}}]$ | D. | $({\frac{10}{3},\frac{13}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com