练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．求函数$f（x）={x^3}-\frac{3}{2}{x^2}+5$在区间[-2，2]上的最大值与最小值．

    分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的最值即可．

    解答 解：f′（x）=3x2-3x=3x（x-1），
    令f′（x）＞0，解得：x＞1或x＜0，
    令f′（x）＜0，解得：0＜x＜1，
    故f（x）在[-2，0）递增，在（0，1）递减，在（1，2]递增，
    而f（-2）=-9，f（0）=5，f（1）=$\frac{9}{2}$，f（2）=7，
    故函数f（x）max=7，f（x）min=f（-2）=-9．

    点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知抛物线C：y2=2px（p＞0）的焦点F与椭圆$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{8}$=$\frac{1}{2}$的一个焦点重合，直线l过点A（4，0）且与抛物线交于P、Q两点．
    （1）求p的值；
    （2）若$\overrightarrow{FP}$+$\overrightarrow{PQ}$=$\overrightarrow{FR}$，试求动点R的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．下列命题中
    ①A+B=$\frac{π}{2}$是sinA=cosB成立的充分不必要条件．
    ②${（\frac{1}{{\sqrt{x}}}-x）^6}$的展开式中的常数项是第4项．
    ③在数列{an}中，a1=2，Sn是其前n项和且满足Sn+1=$\frac{1}{2}{S_n}$+2，则数列{an}为等比数列．
    ④设过函数f（x）=x2-x（-1≤x≤1）图象上任意一点的切线的斜率为K，则K的取值范围是（-3，1）
    把你认为正确的命题的序号填在横线上①③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．由正整数组成的一组数据x1，x2，x3，x4，其平均数和中位数都是2，且标准差等于$\frac{{\sqrt{2}}}{2}$，则这组数据为1，2，2，3． （从小到大排列）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知过点（0，-2$\sqrt{3}$），斜率为$\sqrt{3}$的直线l过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点，椭圆C的中心关于直线l的对称点在直线x=$\frac{{a}^{2}}{2}$上．
    （1）求椭圆C的方程；
    （2）过点E（-2，0）的直线m交椭圆C于点M、N，且满足tan∠MON=$\frac{4\sqrt{6}}{3\overrightarrow{OM}•\overrightarrow{ON}}$（O为坐标原点），求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

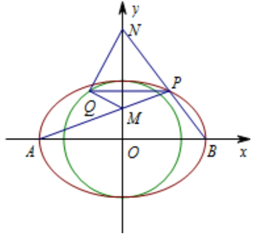    10．已知椭圆C：$\frac{x^2}{4}+\frac{y^2}{b^2}=1$（b＞0），以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点，A，B是椭圆C的长轴端点．
    （1）求圆O的方程和椭圆C的离心率e；
    （2）设P，Q分别是椭圆C和圆O上的动点（P，Q位于y轴两侧），且直线PQ与x轴平行，直线AP，BP分别与y轴交于点M，N，试判断MQ与NQ所在的直线是否互相垂直，若是，请证明你的结论；若不是，也请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．以下四个命题中是假命题的是（　　）
    A．“昆虫都是6条腿，竹节虫是昆虫，所以竹节虫有6条腿”此推理属于演绎推理．
    B．“在平面中，对于三条不同的直线a，b，c，若a∥b，b∥c则a∥c，将此结论放到空间中也成立”此推理属于合情推理．
    C．“a≤0”是“函数f（x）=ax+lnx存在极值”的必要不充分条件．
    D．若$x∈（0\;，\;\;\frac{π}{2}]$，则$sinx+\frac{2}{sinx}$的最小值为$2\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知：复数z1=2sinAsinC+（a+c）i，z2=1+2cosAcosC+4i，且z1=z2，其中A、B、C为△ABC的内角，a、b、c为角A、B、C所对的边．
    （Ⅰ）求角B的大小；
    （Ⅱ） 若$b=2\sqrt{2}$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知双曲线${x^2}-\frac{y^2}{b^2}=1（{b＞0}）$，以原点O为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A，B，C，D四点，这四点围成的四边形面积为b，则双曲线的离心率为（　　）
    A．$\sqrt{3}$B．2C．3D．$2\sqrt{2}$

    查看答案和解析>>

    同步练习册答案