
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
分析 根据题意,点(3,4)到原点的距离等于半焦距,可得a2+b2=25.由点(3,4)在双曲线的渐近线上,得到$\frac{b}{a}$=$\frac{4}{3}$,两式联解得出a=3且b=4,即可得到所求双曲线的方程.
解答 解:∵点(3,4)在以|F1F2|为直径的圆上,
∴c=5,可得a2+b2=25…①
又∵点(3,4)在双曲线的渐近线y=$\frac{b}{a}$x上,
∴$\frac{b}{a}$=$\frac{4}{3}$…②,
①②联解,得a=3且b=4,
可得双曲线的方程$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1.
故选:C.
点评 本题给出双曲线满足的条件,求双曲线的方程,考查了双曲线的标准方程与简单几何性质,主要是渐近线方程的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
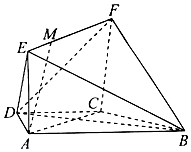 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 33 | C. | $\sqrt{31}$ | D. | $\sqrt{33}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.
某年级480名学生在一次面米测试中,成绩全部介于13秒和18秒之间,将测试结果分成5组,如图为其频率分布直方图,如果从左到右的5个小矩形的面积之比为1:3:7:6:3,那么成绩在[16,18]的学生人数是216.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿”此推理属于演绎推理. | |
| B. | “在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也成立”此推理属于合情推理. | |
| C. | “a≤0”是“函数f(x)=ax+lnx存在极值”的必要不充分条件. | |
| D. | 若$x∈(0\;,\;\;\frac{π}{2}]$,则$sinx+\frac{2}{sinx}$的最小值为$2\sqrt{2}$. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com