
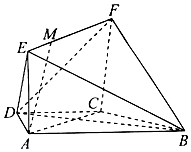
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.分析 (Ⅰ)由已知,若证得AC⊥BC,则据面面垂直的性质定理即可.转化成在平面ABCD,能否有AC⊥BC,易证成立.
(Ⅱ)设AC∩BD=N,则面AMF∩平面BDF=FN,只需AM∥FN即可.而CN:NA=1:2.故应有EM:FM=1:2
解答 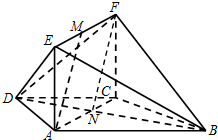 (Ⅰ)证明:在梯形ABCD中,
(Ⅰ)证明:在梯形ABCD中,
∵AD=DC=CB=a,∠ABC=60°
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=90°,∴AC⊥BC,
又∵平面ACF⊥平面ABCD,交线为AC,∴BC⊥平面ACFE.
(Ⅱ)当EM=$\frac{\sqrt{3}}{3}$a时,AM∥平面BDF.
在梯形ABCD中,设AC∩BD=N,连接FN,则CN:NA=1:2.
∵EM=$\frac{\sqrt{3}}{3}$a而EF=AC=$\sqrt{3}$a,∴EM:FM=1:2.∴EM∥CN,EM=CN,
∴四边形ANFM是平行四边形.∴AM∥NF.
又NF?平面BDF,AM?平面BDF.∴AM∥平面BDF.
点评 本题考查线面位置关系及判定,考查空间想象能力,计算能力,转化能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 3 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com