
分析 (1)联立 $\left\{\begin{array}{l}{y=a}\\{y=\frac{{x}^{2}}{4}}\end{array}\right.$,可得交点M,N的坐标,由曲线C:y=$\frac{{x}^{2}}{4}$,利用导数的运算法则可得:y′=$\frac{x}{2}$,利用导数的几何意义、点斜式即可得出切线方程.
(2)存在符合条件的点(0,-a),设P(0,b)满足∠OPM=∠OPN.M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为:k1,k2.直线方程与抛物线方程联立化为x2-4kx-4a=0,利用根与系数的关系、斜率计算公式可得k1+k2=$\frac{k(a+b)}{a}$.k1+k2=0?直线PM,PN的倾斜角互补?∠OPM=∠OPN.即可证明.
解答 解:(1)联立 $\left\{\begin{array}{l}{y=a}\\{y=\frac{{x}^{2}}{4}}\end{array}\right.$,可得$M(2\sqrt{a},a)$,$N(-2\sqrt{2},a)$,或$M(-2\sqrt{2},a)$,$N(2\sqrt{a},a)$.
∵$y'=\frac{1}{2}x$,故$y=\frac{x^2}{4}$在x=$2\sqrt{2}a$处的到数值为$\sqrt{a}$,
C在$(2\sqrt{2}a,a)$处的切线方程为$y-a=\sqrt{a}(x-2\sqrt{a})$,即$\sqrt{a}x-y-a=0$.
故$y=\frac{x^2}{4}$在x=-$2\sqrt{2}a$处的导数值为-$\sqrt{a}$,
C在$(-2\sqrt{2}a,a)$处的切线方程为$y-a=-\sqrt{a}(x+2\sqrt{a})$,即$\sqrt{a}x+y+a=0$.
故所求切线方程为$\sqrt{a}x-y-a=0$或$\sqrt{a}x+y+a=0$.
(2)存在符合题意的点,证明如下:
设P(0,b)为复合题意得点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为k1,k2.
将y=kx+a代入C得方程整理得x2-4kx-4a=0.
∴x1+x2=4k,x1x2=-4a.
∴${k_1}+{k_2}=\frac{{{y_1}-b}}{x_1}+\frac{{{y_2}-b}}{x_2}$=$\frac{{2k{x_1}{x_2}+(a-b)({x_1}+{x_2})}}{{{x_1}{x_2}}}$=$\frac{k(a+b)}{a}$.
当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,
故∠OPM=∠OPN,所以P(0,-a)符合题意.
点评 本题考查了导数的运算法则、利用导数的几何意义研究切线方程、直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“log2a>log2b”的充要条件 | |
| B. | 若函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到的函数图象关于y轴对称 | |
| C. | 命题“在△ABC中,$A>\frac{π}{3}$,则$sinA>\frac{{\sqrt{3}}}{2}$”的逆否命题为真命题 | |
| D. | 若数列{an}的前n项和为${S_n}={2^n}$,则数列{an}是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
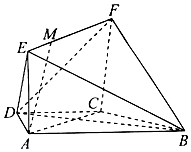 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 55 | C. | 44 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com