
分析 (1)根据导数的运算法则求出函数的导数即可;
(2)求出a的值,解故导函数的不等式,求出函数的单调区间,从而求出函数的最大值和最小值即可;
(3)根据二次函数的性质得到关于a的不等式组,解出即可.
解答 解:(1)由原式得f(x)=x3-ax2-4x+4a,
∴f'(x)=3x2-2ax-4.
(2)由f'(-1)=0,得$a=\frac{1}{2}$,
所以$f(x)={x^3}-\frac{1}{2}{x^2}-4x+2$,
f'(x)=3x2-x-4.
由f'(x)=0,得$x=\frac{4}{3}$或x=-1.
又$f({\frac{4}{3}})=-\frac{50}{27}$,$f(-1)=\frac{9}{2}$,f(-2)=0,f(2)=0,
∴f(x)在[-2,2]上的最大值为$\frac{9}{2}$,最小值为$-\frac{50}{27}$.
(3)f'(x)=3x2-2ax-4的图象为开口向上且过点(0,-4)的抛物线,
由条件得f'(-2)≥0,f'(2)≥0,
即$\left\{\begin{array}{l}4a+8≥0\\ 8-4a≥0.\end{array}\right.$∴-2≤a≤2,
∴a的取值范围为[-2,2].
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及二次函数的性质,是一道中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{12}+\frac{y^2}{11}=1$ | B. | $\frac{x^2}{36}-\frac{y^2}{35}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
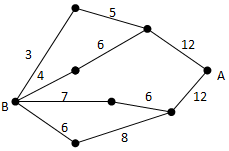 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 120 | C. | 144 | D. | 192 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
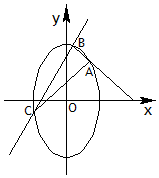 如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.
如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com