
分析 (1)利用等可能事件概率计算公式能求出甲中奖的概率.
(2)利用相互独立事件概率乘法公式能求出甲、乙都中奖的概率.
(3)利用对立事件概率计算公式能求出甲、乙至少有一个中奖的概率
解答 解:(1)一盒有10张奖券,其中2张是有奖的,先由甲后由乙各抽一张,
设“甲中奖”为事件A,
∴甲中奖的概率为$P(A)=\frac{2}{10}=\frac{1}{5}$.
(2)设“甲、乙都中奖”为事件B,
∴甲、乙都中奖的概率$P(B)=\frac{2}{10×9}=\frac{1}{45}$.
(3)设“甲、乙至少有一人中奖”为事件C,
甲、乙至少有一个中奖的概率:
$P(C)=1-\frac{8×7}{10×9}=1-\frac{56}{90}=\frac{17}{45}$….(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式、相互独立事件概率乘法公式、对立事件概率计算公式的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“log2a>log2b”的充要条件 | |
| B. | 若函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到的函数图象关于y轴对称 | |
| C. | 命题“在△ABC中,$A>\frac{π}{3}$,则$sinA>\frac{{\sqrt{3}}}{2}$”的逆否命题为真命题 | |
| D. | 若数列{an}的前n项和为${S_n}={2^n}$,则数列{an}是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
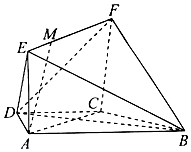 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 33 | C. | $\sqrt{31}$ | D. | $\sqrt{33}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com