
已知两点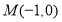 、
、 ,点
,点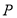 为坐标平面内的动点,满足
为坐标平面内的动点,满足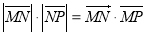 .
.
(1)求动点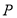 的轨迹方程;
的轨迹方程;
(2)若点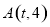 是动点
是动点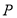 的轨迹上的一点,
的轨迹上的一点,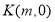 是
是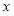 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线
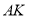 与圆
与圆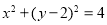 的位置关系.
的位置关系.
(1) (2)当
(2)当 时,直线
时,直线 与圆
与圆 相交;当
相交;当 时,直线
时,直线 与圆
与圆 相切;当
相切;当 时,直线
时,直线 与圆
与圆 相离.
相离.
【解析】
试题分析:(1)直接法求轨迹:根据题意列出方程化简。(2)将点 代入
代入 求
求 ,求出只直线
,求出只直线 方程注意讨论其斜率存在与否。求圆心到直线
方程注意讨论其斜率存在与否。求圆心到直线 的距离,根据距离与半径的关系判断直线与圆的关系。
的距离,根据距离与半径的关系判断直线与圆的关系。
试题解析:(1)设 ,则
,则 ,
,
 ,
,
 . 2分
. 2分
由 ,
,
得2 , 4分
, 4分
化简得 .
.
所以动点 的轨迹方程为
的轨迹方程为 . 5分
. 5分
(2)由点 在轨迹
在轨迹 上,则
上,则 ,解得
,解得 ,即
,即 . 6分
. 6分
当 时,直线
时,直线 的方程为
的方程为 ,此时直线
,此时直线 与圆
与圆 相离. 7分
相离. 7分
当 时,直线
时,直线 的方程为
的方程为 ,即
,即 , 8分
, 8分
圆心 到直线
到直线 的距离
的距离
 ,
,
令

 ,解得
,解得 ;
;
令

 ,解得
,解得 ;
;
令

 ,解得
,解得 .
.
综上所述,当 时,直线
时,直线 与圆
与圆 相交;
相交;
当 时,直线
时,直线 与圆
与圆 相切;
相切;
当 时,直线
时,直线 与圆
与圆 相离. 14分
相离. 14分
考点:1求轨迹方程;2直线与圆的位置关系。


科目:高中数学 来源:2015届江苏省仪征市高二第一学期期末考试数学试卷(解析版) 题型:填空题
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有________根的棉花纤维的长度小于20mm。

查看答案和解析>>
科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末理数学卷(解析版) 题型:选择题
已知等差数列:5,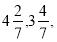 …的前n项和为Sn,则使得Sn取得最大值的n的值为( )
…的前n项和为Sn,则使得Sn取得最大值的n的值为( )
A.7 B.8 C.7或8 D.8或9
查看答案和解析>>
科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:解答题
设集合A={x|x2<9},B={x|(x-2)(x+4)<0}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为A∪B,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:选择题
已知x>0,则y=3x+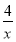 有( )
有( )
A.最大值4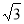 B.最小值4
B.最小值4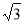 C.最大值2
C.最大值2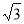 D.最小值2
D.最小值2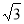
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com