
分析 (1)先求f′(x),再计算f′(0),和f(0),即可得到切线方程;
(2)先求函数的导数f′(x)=axlna+2x-lna=2x+(ax-1)lna,并且f′(0)=0,判断零点两侧的正负,得到单调区间;
(3)将存在性问题转化为|f(x1)-f(x2)|max≥e-1,即f(x)max-f(x)min≥e-1,
根据上一问的单调性得到最小值f(0),再计算端点值f(-1)和f(1)比较大小.因为$f(1)-f(-1)=(a+1-lna)-(\frac{1}{a}+1+lna)=a-\frac{1}{a}-2lna$,再令令$g(a)=a-\frac{1}{a}-2lna(a>0)$,
求其导数,分情况比较大小,计算a的取值范围.
解答 解:(1)因为函数f(x)=ax+x2-xlna(a>0,a≠1),
所以f′(x)=axlna+2x-lna,f′(0)=0,
又因为f(0)=1,所以函数f(x)在点(0,f(0))处的切线方程为y=1;
(2)由(1),f′(x)=axlna+2x-lna=2x+(ax-1)lna.
当a>1时,lna>0,(ax-1)lna在R上递增;
当0<a<1时,lna<0,(ax-1)lna在R上递增;
故当a>0,a≠1时,总有f′(x)在R上是增函数,
又f′(0)=0,所以不等式f′(x)>0的解集为(0,+∞),
故函数f(x)的单调增区间为(0,+∞),递减区间为 (-∞,0);
(3)因为存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1成立,
而当x∈[-1,1]时,|f(x1)-f(x2)|≤f(x)max-f(x)min,
所以只要f(x)max-f(x)min≥e-1即可.
又因为x,f'(x),f(x)的变化情况如下表所示:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 减函数 | 极小值 | 增函数 |
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查分类讨论思想方法和转化思想的运用,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
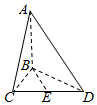 如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )
如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
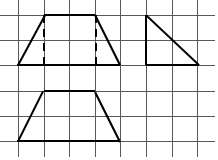
| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{3},\frac{2}{3}]$ | B. | $[\frac{1}{6},\frac{4}{3}]$ | C. | $[\frac{1}{3},\frac{4}{3}]$ | D. | $[\frac{2}{3},\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:
如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩电脑游戏 | 18 | 12 | 30 |
| 不喜欢玩电脑游戏 | 5 | 16 | 21 |
| 总计 | 23 | 28 | 51 |
| A. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| B. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少无关 | |
| C. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| D. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com