
 一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.
一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.分析 (1)以O为原点,正东方向为x正半轴,如图建立直角坐标系,求得A坐标,过O作台风中线运动的直线L的垂线,垂足为H,求得H坐标,即可台风所影响区域的边界曲线方程;
(2)依题意知台风形成后5小时开始影响港口,记以O为圆心,$100\sqrt{5}$为半径的圆与L相交于M,N两点(M离A近),由勾股定理求得HM和AM,即5a=100,即可求得a的中,由MN=2HM=200,t=$\frac{MN}{v}$,即可求得该台风影响持续时间段的长.
解答 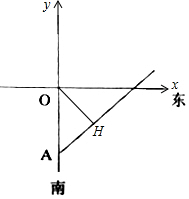 解:(1)以O为原点,正东方向为x正半轴,如图建立直角坐标系,则$A(0,-200\sqrt{2})$,
解:(1)以O为原点,正东方向为x正半轴,如图建立直角坐标系,则$A(0,-200\sqrt{2})$,
过O作台风中线运动的直线L的垂线,垂足为H,
依题意得:OH=200,OH:y=-x,AH:$y=-200\sqrt{2}$
联立求得交点$H(100\sqrt{2},-100\sqrt{2})$,
当台风中心离港口O距离最近时,该台风影响区域的边界曲线方程为圆:${(x-100\sqrt{2})^2}+{(y+100\sqrt{2})^2}=50000$;
(2)(i)依题意知台风形成后5小时开始影响港口,记以O为圆心,$100\sqrt{5}$为半径的圆与L相交于M,N两点(M离A近),
∵$OH=200,OM=100\sqrt{5}$,
∴HM=100,又AH=200,
∴AM=100,于是5a=100,得a=20,
(ii)又MN=2HM=200,
∴t=$\frac{200}{20}=10$,
所以持续时间段的长为10小时.
点评 本题主要考查了解三角形的实际应用.考查了考生运用所学知识解决实际问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com