
分析 (1)f(-1)=|a+8|>f(1)=|a-8|,$f(\frac{4}{a})=\frac{16}{a}≥2$,分类讨论,求函数f(x)在区间[-1,1]上的最大值;
(2)y=|f(x)-2|=||ax2-8x|-2|,对称轴$x=\frac{4}{a}$,分类讨论,利用函数y=|f(x)-2|在区间[0,b]上单调递减,建立不等式,即可求实数b的取值范围.
解答 解:(1)f(-1)=|a+8|>f(1)=|a-8|,$f(\frac{4}{a})=\frac{16}{a}≥2$,
①当0<a≤4时,即$1≤\frac{4}{a}$,则f(x)max=f(-1)=a+8;
②当4<a≤8时,f(x)max=f(-1)=a+8或$f(\frac{4}{a})=\frac{16}{a}$,
当$a+8=\frac{16}{a}$时,$a=4\sqrt{2}-4$,所以当$a>4\sqrt{2}-4$时,f(x)max=f(-1)=a+8.
综上,f(x)max=a+8.
(2)y=|f(x)-2|=||ax2-8x|-2|,对称轴$x=\frac{4}{a}$,
①a≥8时,要使函数y=|f(x)-2|在区间[0,b]上单调递减,
则$[0,b]⊆[0,\frac{4}{a}]$,即$b≤\frac{4}{a}$,
又因为$0<\frac{4}{a}≤\frac{1}{2}$,所以$b≤\frac{1}{2}$;
②当0<a<8时,${x_2}=\frac{{4-\sqrt{16-2a}}}{a}$,要使函数y=|f(x)-2|在区间[0,b]上单调递减,
则$[0,b]⊆[0,\frac{{4-\sqrt{16-2a}}}{a}]$,即$b≤\frac{{4-\sqrt{16-2a}}}{a}=\frac{2}{{4+\sqrt{16-2a}}}$,
又因为$0<\sqrt{16-2a}<4$,∴$4<4+\sqrt{16-2a}<8$,∴$\frac{1}{4}<\frac{2}{{4+\sqrt{16-2a}}}<\frac{1}{2}$,即$b<\frac{1}{2}$.
综上,b≤$\frac{1}{2}$.
点评 本题考查函数的最值,考查函数的单调性,考查学生分析解决问题的能力,考查计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 5 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.
如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,3) | B. | {4,-3} | C. | {(4,3)} | D. | {(4,-3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 技术改造的月份x | 1 | 2 | 3 | 4 |
| 煤炭消耗量y | 4.5 | 4 | 3 | 2.5 |
| A. | $\widehat{y}$=0.7x+5.25 | B. | $\widehat{y}$=-0.6x+5.25 | C. | $\widehat{y}$=-0.7x+6.25 | D. | $\widehat{y}$=-0.7x+5.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
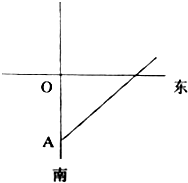 一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.
一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{16}$ | B. | x=-$\frac{1}{16}$ | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com