

分析 (1)棱锥中的垂直关系,在平面图形中分析出来,运用线面垂直的判断定理,证得CD⊥平面ABC,由线面垂直性质,得出DC⊥BE.
(2)由(1)分析位置关系时,易发现BE⊥平面ACD,故EF为BF在平面ACD的投影,∠BFE为所求角,再构造三角形求解.
解答 (Ⅰ)证明:AB是斜边上的高,沿AB将△ACD折成棱锥A-BCD,
有AB⊥BC,AB⊥BD,且BC?平面BCD,BD?平面BCD
∴AB⊥平面BCD. …1分
又CD?平面BCD
∴AB⊥CD. …3分
又CD⊥BC,且AB?平面ABC、BC?平面ABC
∴CD⊥平面ABC. …5分
又∵BE?平面ABC
所以DC⊥BE …6分
(Ⅱ)解:由(Ⅰ)知DC⊥BE,且由题 BE⊥AC,
∴BE⊥平面ACD. …7分
所以BF在平面ACD内的射影就是EF,
∴BF与平面ACD所成的角就是∠BFE,且△BDF为RT△.…8分
∴$sin∠BFE=\frac{BE}{BF}$,…9分
∵在平面图中$\frac{BE}{BF}=\frac{BE}{AE}=\frac{AC}{AD}=\frac{1}{2}$,
∴$sin∠BFE=\frac{1}{2}$ …11分
∴∠BFE=30°,即BF与平面ACD所成的角为30°. …12分
点评 本题考查线面垂直的判定定理及性质,考查了用几何法求线面角(找角--证角--求角).第二问中,发现EF是BF在平面ACD的投影,是解决第二问的关键.本题属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.
如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
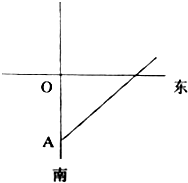 一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.
一台风中心于某天中午12:00在港口O的正南方向,距该港口200$\sqrt{2}$千米的海面A处形成(如图),并以每小时a千米的速度向北偏东45°方向上沿直线匀速运动,距台风中心100$\sqrt{5}$千米以内的范围将受到台风的影响,请建立适当的坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{16}$ | B. | x=-$\frac{1}{16}$ | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
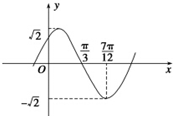 函数f(x)=Asin(?x+φ)(A>0,?>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(?x+φ)(A>0,?>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为( )| A. | $f(x)=\sqrt{2}sin(x+\frac{π}{3})$ | B. | $f(x)=\sqrt{2}sin(x-\frac{π}{3})$ | C. | $f(x)=\sqrt{2}sin(2x+\frac{π}{3})$ | D. | $f(x)=\sqrt{2}sin(2x-\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com