
设函数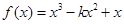
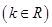 .
.
(1) 当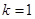 时,求函数
时,求函数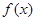 的单调区间;
的单调区间;
(2) 当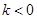 时,求函数
时,求函数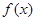 在
在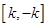 上的最小值
上的最小值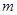 和最大值
和最大值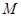 .
.
(1) 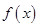 在
在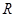 上单调递增
上单调递增
(2) 当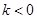 时,
时,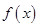 的最小值
的最小值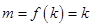 ,最大值
,最大值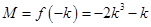
【解析】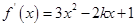
(1)当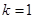 时
时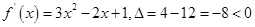
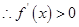 ,
,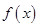 在
在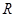 上单调递增.
上单调递增.
(2)当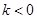 时,
时,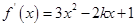 ,其开口向上,对称轴
,其开口向上,对称轴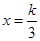 ,且过
,且过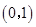
(i)当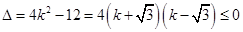 ,即
,即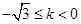 时,
时,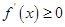 ,
,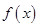 在
在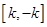 上单调递增,
上单调递增,
从而当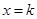 时,
时,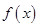 取得最小值
取得最小值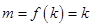 ,
,
当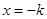 时,
时,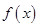 取得最大值
取得最大值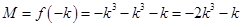 .
.

(ii)当 ,即
,即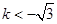 时,令
时,令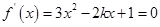
解得: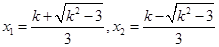 ,注意到
,注意到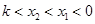 ,
,
(注:可用韦达定理判断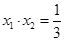 ,
,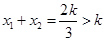 ,从而
,从而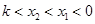 ;或者由对称结合图像判断)
;或者由对称结合图像判断)
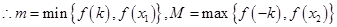
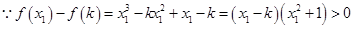
 的最小值
的最小值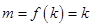 ,
,
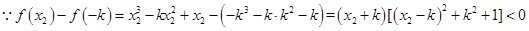
 的最大值
的最大值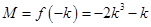
综上所述,当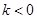 时,
时,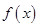 的最小值
的最小值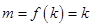 ,最大值
,最大值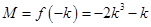
解法2(2)当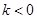 时,对
时,对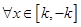 ,都有
,都有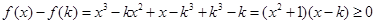 ,
,
故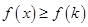
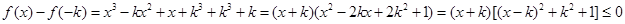
故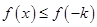 ,而
,而 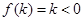 ,
,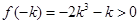
所以 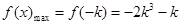 ,
,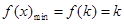
(1)根据k的取值化简函数的表达式,明确函数的定义域,然后利用求导研究函数的单调区间,中规中矩;(2)借助求导,通过对参数K的正负讨论和判别式的讨论进行分析求解最值.
【考点定位】本题考查函数的单调性和函数的最值问题,考查学生的分类讨论思想和构造函数的解题能力.


科目:高中数学 来源: 题型:
| 1-x |
| x+3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com