
分析 求定积分得到a的值,再利用二项式定理把(2x-$\frac{1}{x}$)5 展开,可得(x+$\frac{a}{x}$)(2x-$\frac{1}{x}$)5的展开式中的常数项.
解答 解:∵a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx=lnx${|}_{1}^{{e}^{2}}$=2,则二项式(x+$\frac{a}{x}$)(2x-$\frac{1}{x}$)5=(x+$\frac{2}{x}$)(2x-$\frac{1}{x}$)5
=(x+$\frac{2}{x}$)•(${C}_{5}^{0}$•(2x)5+${C}_{5}^{1}$•(2x)4•(-$\frac{1}{x}$)+${C}_{5}^{2}$•(2x)3•${(-\frac{1}{x})}^{2}$+${C}_{5}^{3}$•(2x)2•${(-\frac{1}{x})}^{3}$+${C}_{5}^{4}$•(2x)•${(-\frac{1}{x})}^{4}$+${C}_{5}^{5}$(-$\frac{1}{x}$)5 ,
=(x+$\frac{2}{x}$)•(32x5-80x3+80x-40•$\frac{1}{x}$+10•$\frac{1}{{x}^{3}}$-$\frac{1}{{x}^{5}}$),
故展开式中的常数项为-40+2•80=120,
故答案为:120.
点评 本题主要考查定积分、二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338 石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2\sqrt{2},+∞)$ | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,3) | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
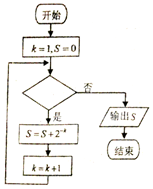
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com