
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 由增加的长度决定 |
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
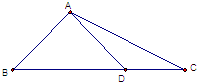
| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | 大于300 |
| 空气质量级别 | Ⅰ级(优) | Ⅱ级(良) | Ⅲ1(轻微污染) | Ⅲ2(轻度污染) | Ⅳ1(中度污染) | Ⅳ2(中度重污染) | Ⅴ(重度污染) |
| 分组 | 频数统计 | 频数 | 频率 |
| 0~50 | 0.30 | ||
| 51~100 |  | 12 | 0.40 |
| 101~150 | |||
| 151~200 |  | 3 | 0.10 |
| 201~250 |  | 3 | 0.10 |
| 合计 | 30 | 30 | 1.00 |
查看答案和解析>>
科目:高中数学 来源:2017届广西陆川县中学高三9月月考数学(文)试卷(解析版) 题型:选择题
已知两个不同的平面 和两条不重合的直线
和两条不重合的直线 ,则下列四个命题中不正确的是( )
,则下列四个命题中不正确的是( )
A.若 ,则
,则
B.若 ,则
,则
C.若 ,则
,则
D.若 ,则
,则
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com