练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知sinθcosθ＜0，那么角θ是（　　）
    A．第一或第二象限角B．第二或第三象限角
    C．第二或第四象限角D．第一或第四象限角

    分析 根据题意列出不等式组，由三角函数值的符号判断出θ所在的象限．

    解答 解：由题意知，sinθcosθ＜0，
    则$\left\{\begin{array}{l}{sinθ＞0}\\{cosθ＜0}\end{array}\right.$或$\left\{\begin{array}{l}{sinθ＜0}\\{cosθ＞0}\end{array}\right.$，所以角θ在第二或第四象限，
    故选：C．

    点评 本题考查角函数值的符号的应用，需要掌握口诀：一全正、二正弦、三正切、四余弦，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．$\frac{1}{2}+（{\frac{1}{2}+\frac{1}{4}}）+（{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}}）+…+（{\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{10}}}}}）$的值为（　　）
    A．7+$\frac{1}{2^9}$B．9+$\frac{1}{{{2^{10}}}}$C．11+$\frac{1}{{{2^{11}}}}$D．7+$\frac{1}{{{2^{10}}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”，计算得到统计量值k2的观测值k≈4.892，参照下表，得到的正确结论是（　　）
     P（k2≥k） 0.10 0.05 0.010
     k 2.706 3.841 6.635
    A．在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别有关”
    B．在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别无关”
    C．有99%以上的把握认为“爱好该运动与性有关”
    D．有99%以上的把握认为“爱好该运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．若x∈R+，则x+$\frac{4}{x}$的最小值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

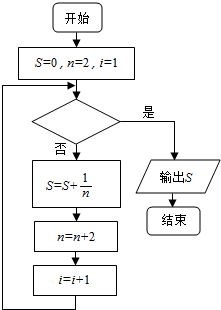    20．如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图，则判断框内应填入关于i的不等式为（　　）
    A．i＜50B．i＞50C．i＜51D．i＞51

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=4，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°．
    （1）若$\overrightarrow{a}$⊥（k$\overrightarrow{a}$+$\overrightarrow{b}$），求实数k的值；
    （2）求$\overrightarrow{a}$+2$\overrightarrow{b}$的模．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．某校为了了解高三同学暑假期间学习情况，调查了200名同学，统计他们每天平均学习时间，绘成频率分布直方图（如图）．则这200名同学中学习时间在6～8小时的同学为60人．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列说法正确的是（　　）
    A．已知购买一张彩票中奖的概率为$\frac{1}{1000}$，则购买1000张这种彩票一定能中奖
    B．互斥事件一定是对立事件
    C．二进制数1101（2）转化为十进制数是13
    D．若样本x1，x2…xn的方差为4，则样本x1-1，x2-1，…，xn-1的方差为3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知△ABC的三条边长分别为3，4，5，如果把三角形的三边都增加相同的长度，则这个新三角形的形状为（　　）
    A．锐角三角形B．直角三角形
    C．钝角三角形D．由增加的长度决定

    查看答案和解析>>

    同步练习册答案