
| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
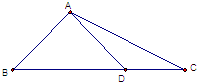
分析 运用向量的数量积的定义,结合条件可得$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|cos∠DAC,再由诱导公式可得$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|sin∠BAC,结合三角形ABC中的正弦定理和直角三角形的锐角三角函数的定义,计算即可得到所求值
解答 解:$\overrightarrow{AD}$•$\overrightarrow{AC}$=$|\overrightarrow{AD}||\overrightarrow{AC}|cos∠CAD$,
∵|$\overrightarrow{AD}$|=1,
∴$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|cos∠CAD,
∵∠BAC=$\frac{π}{2}$+∠DAC,
∴cos∠CAD=sin∠BAC,
$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|sin∠BAC,
在△ABC中,由正弦定理得$\frac{AC}{sinB}=\frac{BC}{sinBAC}$,变形得|AC|sin∠BAC=|BC|sinB,
所以$\overrightarrow{AD}$•$\overrightarrow{AC}$=|$\overrightarrow{AC}$|sin∠BAC=|BC|sinB=|BC|•$\frac{AD}{BD}$=$\sqrt{3}$,
故选A.
点评 本题考查向量的数量积的定义和性质,同时考查诱导公式和正弦定理的运用,属于中档题


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| P(k2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别有关” | |
| B. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该运动与性有关” | |
| D. | 有99%以上的把握认为“爱好该运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知购买一张彩票中奖的概率为$\frac{1}{1000}$,则购买1000张这种彩票一定能中奖 | |
| B. | 互斥事件一定是对立事件 | |
| C. | 二进制数1101(2)转化为十进制数是13 | |
| D. | 若样本x1,x2…xn的方差为4,则样本x1-1,x2-1,…,xn-1的方差为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 由增加的长度决定 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:解答题
在 中,角
中,角 ,
, ,
,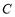 所对的边分别为
所对的边分别为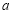 ,
, ,
, ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求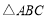 的周长的取值范围.
的周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com