
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据函数的单调性判断①③,根据导函数的根的情况判断②,特殊值法判断④.
解答 解:函数f(x)=x3+ax2+bx+c,f′(x)=3x2+2ax+b,△=4(a2-3b),
若△≤0,则f(x)单调递增或单调递减,若△>0,f(x)可能递减、递增、递减,或递增、递减、递增;
①函数f(x)与x轴一定存在交点;①正确;
②当a2-3b>0时,即△>0,函数f(x)既有极大值也有极小值;②正确;
③若x0是f(x)的极小值点,可能f(x)递减、递增、递减,则f(x)在区间(-∞,x0)不一定单调递减;③错误;
④若f′(x0)=0,则x0是f(x)的极值点;④错误,比如a=b=c=0时,f(x)=x3,f(0)=0,却不是极值点;
故选:B.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 下图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
下图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:| A. | ①④ | B. | ①② | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,$f({x_2})>-\frac{1}{2}$ | B. | f(x1)<0,$f({x_2})<\frac{1}{2}$ | C. | f(x1)>0,$f({x_2})<-\frac{1}{2}$ | D. | f(x1)>0,$f({x_2})>\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
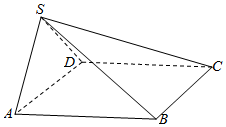 如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.
如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com