
若实数a,b,c,d满足︱b+a2-3lna︱+(c-d+2)2=0,则(a-c)2+(b-d)2的最小值为 .
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:填空题
如图,△OAB是边长为2的正三角形,记△OAB位于直线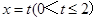 左侧的图形的面积为
左侧的图形的面积为 ,则
,则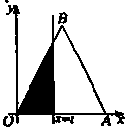
(1)函数 的解析式为_______;
的解析式为_______;
(2)函数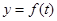 的图像与直线
的图像与直线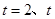 轴围成的图形面积为______.
轴围成的图形面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列结论中正确命题的序号是(写出所有正确命题的序号).
①积分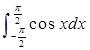 的值为2;②若
的值为2;②若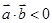 ,则
,则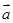 与
与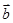 的夹角为钝角;③若
的夹角为钝角;③若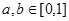 ,则不等式
,则不等式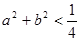 成立的概率是
成立的概率是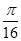 ;④函数
;④函数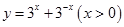 的最小值为2.
的最小值为2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com