
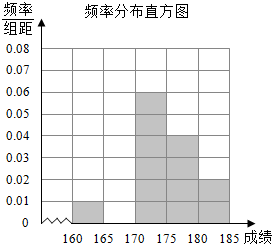
分析 (1)利用$\frac{频率}{组距}=0.07$,然后画出频率分布直方图.
(2)求出第3、4、5组分别抽取3人、2人、1人.基本事件构成集合Ω元素个数,在同一分数段内的事件所含基本事件个数,求出概率.
解答 解:(1)因为各组的频率和等于1,故第2组的频率:f2=1-(0.01+0.06+0.04+0.02)×5=0.35
$\frac{频率}{组距}=0.07$
其频率分布直方图如图所示.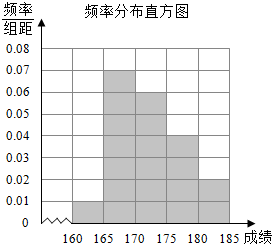
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:$\frac{30}{60}×6=3$人,第4组:$\frac{20}{60}×6=2$人,
第5组:$\frac{10}{60}×6=1$人,
所以第3、4、5组分别抽取3人、2人、1人.
将[170,175)分数段的3人编号为A、B、C,将[50,60)[175,180)分数段的2人编号1、2,[180,185]分数段的1人编号为P从中任取两人,则基本事件构成集合Ω={{A,B},{A,C}{A,1},{A,2},{A,P},{B,C},{B,1},{B,2},{B,P},{C,1},{C,2},{C,P},{1,2},{1,P},{2,P}}共有15个,其中,在同一分数段内的事件所含基本事件为{A,B},{A,C}{B,C},{1,2},共4个,故概率$p=\frac{4}{15}$.
点评 本题考查频率分布直方图的应用,古典概型概率的求法,是基础题.


科目:高中数学 来源: 题型:选择题
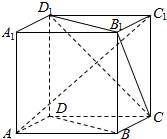
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com