
分析 解:(Ⅰ)直接利用赋值法求得
(Ⅱ)由f(x)是[-1,1]上的奇函数得f(x+$\frac{1}{2}$)<f(1-x),又f(x)在[-1,1]上递增$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$
解答 解:(Ⅰ)f(4)=f(2×2)=f(2)+f(2)=2
∴2f(2)=2⇒f(2)=1
又∵f(2)=f($\sqrt{2}•\sqrt{2}$)=f($\sqrt{2}$)+f($\sqrt{2}$)═
∴2f($\sqrt{2}$)=1⇒f($\sqrt{2}$)=$\frac{1}{2}$
(Ⅱ)由f(x)是[-1,1]上的奇函数得f(x+$\frac{1}{2}$)<f(1-x)
又f(x)在[-1,1]上递增
$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$解得$0≤x<\frac{1}{4}$
∴不等式解集为[0,$\frac{1}{4}$)
点评 本题考查了抽象函数的赋值法,及抽象函数不等式的解法,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)是奇函数,函数g(x)是偶函数 | |
| B. | 函数f(x)不是奇函数,函数g(x)是偶函数 | |
| C. | 函数f(x)是奇函数,函数g(x)不是偶函数 | |
| D. | 函数f(x)不是奇函数,函数g(x)不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {2,4,5} | C. | {1,2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
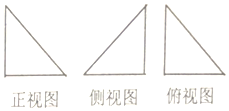 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )| A. | 16π | B. | 3π | C. | $4\sqrt{3}π$ | D. | 12π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com