
���� ��1���������֪��������x���ϣ�����A��2��0����B��0��1�����㣬��a=2��b=1��c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$��������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$�����������ԲC�ķ��̼������ʣ�
��2����ֱ��l�ķ���Ϊy=k��x+2����������Բ���̣���Τ�ﶨ�����е����깫ʽ������е�M�����꣬���࣬�ٵ�k=0ʱ����B������Ϊ��2��0������$\overrightarrow{QA}$•$\overrightarrow{QB}$=4����y0=��2$\sqrt{2}$���ڵ�k��0ʱ���߶�AB�Ĵ�ֱƽ���߷���Ϊy-$\frac{2k}{1+4k2}$=-$\frac{1}{k}$��x+$\frac{8k2}{1+4k2}$�����������������������ʾ������������y0��ֵ��
��� �⣺��1��������ã���ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������x���ϣ�
����A��2��0����B��0��1�����㣮
��a=2��b=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$��
��������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��
��2���ɣ�1����֪A��-2��0����
��B�������Ϊ��x1��y1����ֱ��l��б��Ϊk����ֱ��l�ķ���Ϊy=k��x+2����
����A��B������������㷽����$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$��
�ɷ�������ȥy���������ã�1+4k2��x2+16k2x+��16k2-4��=0��
��-2x1=$\frac{16k2-4}{1+4k2}$����x1=$\frac{2-8k2}{1+4k2}$��
�Ӷ�y1=$\frac{4k}{1+4k2}$��
���߶�AB���е�ΪM��
��M��������-$\frac{8k2}{1+4k2}$��$\frac{2k}{1+4k2}$����
���·����������
�ٵ�k=0ʱ����B������Ϊ��2��0�����߶�AB�Ĵ�ֱƽ����Ϊy�ᣬ����$\overrightarrow{QA}$=��-2��-y0����$\overrightarrow{QB}$=��2��-y0����
��$\overrightarrow{QA}$•$\overrightarrow{QB}$=4����y0=��2$\sqrt{2}$��
�ڵ�k��0ʱ���߶�AB�Ĵ�ֱƽ���߷���Ϊ
y-$\frac{2k}{1+4k2}$=-$\frac{1}{k}$��x+$\frac{8k2}{1+4k2}$����
��x=0�����y0=-$\frac{6k}{1+4k2}$��
��$\overrightarrow{QA}$=��-2��-y0����$\overrightarrow{QB}$=��x1��y1-y0����
$\overrightarrow{QA}$•$\overrightarrow{QB}$=-2x1-y0��y1-y0��
=$\frac{-2?2-8k2?}{1+4k2}$+$\frac{6k}{1+4k2}$��$\frac{4k}{1+4k2}$+$\frac{6k}{1+4k2}$��
=$\frac{4?16k4+15k2-1?}{?1+4k2?2}$=4��
������7k2=2����k=��$\frac{\sqrt{14}}{7}$������y0=��$\frac{2\sqrt{14}}{5}$��
���ϣ�y0=��2$\sqrt{2}$��y0=��$\frac{2\sqrt{14}}{5}$��
���� ���⿼����Բ�ı����̼��������ʣ�����Τ�ﶨ�����е����깫ʽ���������������������㣬������������������е��⣮


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
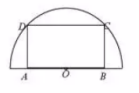 ��ͼ���ڰ뾶Ϊ40cm�İ�Բ�Σ�OΪԲ�ģ���Ƥ�Ͻ�ȡһ����β���ABCD������A��B��ֱ���ϣ���C��D��Բ���ϡ�
��ͼ���ڰ뾶Ϊ40cm�İ�Բ�Σ�OΪԲ�ģ���Ƥ�Ͻ�ȡһ����β���ABCD������A��B��ֱ���ϣ���C��D��Բ���ϡ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1] | B�� | ��-1��1�� | C�� | ��-1��1] | D�� | ��-1��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 576�� | B�� | 504�� | C�� | 288�� | D�� | 252�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com